2023-2024学年四川省绵阳市涪城区南山中学高一（上）开学数学试卷

一、选择题：本大题共12小题，每小题3分，共36分，在每小题给出的四个选项中，只有一个是符合题目要求的.

• 1．

  81

  的平方根是（　　）

  A．±9

  B．±3

  C．9

  D．3
  组卷：365引用：3难度：0.9

  解析

• 2．下列各式，运算正确的是（　　）

  A．（-a3）2=a5	B． （ a 3 ） 3 = a 3 9
  C．a2•a4=a6	D．2a3b3-a2b2=ab
  组卷：85引用：2难度：0.9

  解析

• 3．有一正方体，六个面上分别写有数字1、2、3、4、5、6，有三个人从不同的角度观察的结果如图所示．如果记数字6对面的数字为a,数字2对面的数字为b,那么a+b的值为（　　）
  ​

  A．3

  B．7

  C．8

  D．11
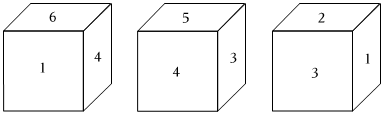  组卷：11引用：2难度：0.8

  解析

• 4．点M（x₁，y₁），N（x₂，y₂）在反比例函数

  y

  =

  -

  3

  x

  的图象上，且x₁＜0＜x₂，则（　　）

  A．y1＞0＞y2

  B．y1＜0＜y2

  C．y1＞y2＞0

  D．y1＜y2＜0
  组卷：8引用：2难度：0.9

  解析

• 5．设全集U={1，2，3，4，5，6，7，8}，集合A={1，2，3，5}，B={2，4，6}，则图中的阴影部分表示的集合为（　　）

  A．{2}

  B．{4，6}

  C．{1，3，5}

  D．{4，6，7，8}
  组卷：1128引用：85难度：0.9

  解析

• 6．在Rt△ABC中，∠C=90°，AC=4，BC=7，点D在边BC上，CD=3，⊙A的半径长为3，若⊙D与⊙A相切，且点B在⊙D内，则⊙D的半径长度为（　　）

  A．2或8

  B．5或8

  C．5

  D．8
  组卷：7引用：2难度：0.8

  解析

• 7．数据x₁，x₂，x₃…，x_n分别是某学校教职工n（n≥3，n∈N*）个人的年收入，设这n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入数据x_n+1，则对这（n+1）个数据，下列说法正确的是（　　）

  A．年收入平均数增大，中位数可能不变，方差变大

  B．年收入平均数增大，中位数一定变大，方差变大

  C．年收入平均数增大，中位数可能不变，方差可能不变

  D．年收入平均数可能不变，中位数可能不变，方差可能不变
  组卷：43引用：2难度：0.8

  解析

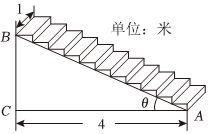• 8．一座楼梯的示意图如图所示，BC是铅垂线，CA是水平线，BA与CA的夹角为θ．现要在楼梯上铺一条地毯，已知CA=4米，楼梯宽度1米，则地毯的面积至少需要（　　）

  A． 4 sinθ 米 2	B． 4 cosθ 米2
  C． （ 4 + 4 tanθ ） 米 2	D．（4+4tanθ）米2
  组卷：29引用：2难度：0.7

  解析

三、解答题：共7小题，满分90分.解答应写出必要的文字说明、证明过程或演算步骤.

• 24．如图，抛物线y=ax²+3ax+c（a＞0）与y轴交于点C，与x轴交于A、B两点，A点在B点左侧．点B的坐标为（1，0），OC=3OB．
  
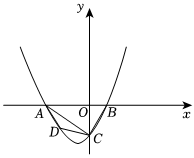
  （1）求抛物线的解析式；
  （2）若点D是线段AC下方抛物线上的动点，求四边形ABCD面积的最大值；
  （3）若点E在x轴上，点P在抛物线上．是否存在以A、C、E、P为顶点且以AC为一边的平行四边形？若存在，求点P的坐标；若不存在，请说明理由．
  组卷：18引用：2难度：0.5

  解析

• 25．如图1，已知直线EA与x轴、y轴分别交于点E和点A（0，2），过直线EA上的两点F、G分别作x轴的垂线段，垂足分别为M（m,0）和N（n,0），其中m＜0，n＞0．
  （1）如果m=-4，n=1，试判断△AMN的形状；
  （2）如果mn=-4，（1）中有关△AMN的形状的结论还成立吗？如果成立，请证明；如果不成立，请说明理由；
  （3）如图2，题目中的条件不变，如果mn=-4，并且ON=4，求经过M、A、N三点的抛物线所对应的函数关系式；
  （4）在（3）的条件下，如果抛物线的对称轴l与线段AN交于点P，点Q是对称轴上一动点，以点P、Q、N为顶点的三角形和以点M、A、N为顶点的三角形相似，求符合条件的点Q的坐标．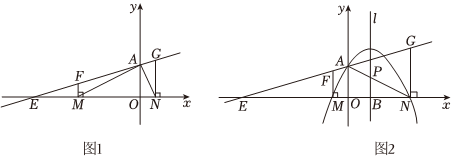
  
  组卷：17引用：2难度：0.3

  解析