当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省苏州中学高一（下）月考数学试卷（3月份）

发布：2024/6/21 8:0:10

一、单项选择题：本小题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知平面向量
a
=（2，4），
b
=（-3，m+2），
a
∥
b
，则m=（　　）
A．-2 B．-8 C．6 D．4
组卷：96引用：2难度：0.8
解析
2．《九章算术》是我国算术名著，其中有这样一个问题：“今有宛田，下周三十步，径十六步，问为田几何？”意思是说：现有扇形田，弧长三十步，直径十六步，问面积多少？书中给出计算方法，以径乘周，四而一，即扇形的面积等于直径乘以弧长再除以4，在此问题中，扇形的圆心角的弧度数是（　　）
A．
4
15
B．
15
4
C．
15
8
D．120
组卷：702引用：10难度：0.8
解析
3．已知函数f（x）=sinxcos（2x+φ）（φ∈[0，π]）为偶函数，则φ=（　　）
A．0 B．
π
4
C．
π
2
D．π
组卷：372引用：3难度：0.8
解析
4．已知
a
=
（
-
2
，-
1
）
，
b
=
（
λ
，
1
）
，则λ＞-
1
2
是“
a
与
b
的夹角为钝角”的（　　）条件
A．充分不必要 B．必要不充分
C．充分必要 D．既不充分也不必要
组卷：377引用：8难度：0.8
解析
5．若点P（cosα，sinα）在直线y=-2x上，则sin²α+cos（2α+
π
2
）=（　　）
A．0 B．
2
5
C．
6
5
D．
8
5
组卷：181引用：5难度：0.9
解析
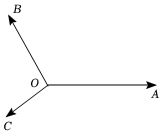6．如图所示，平面内有三个向量
OA
，
OB
，
OC
，
OA
与
OB
的夹角为120°，
OA
与
OC
的夹角为150°，且
|
OA
|
=
|
OB
|
=
1
，
|
OC
|
=
3
3
，若
OB
=
λ
OA
+
μ
OC
（λ，μ∈R），则λ+μ=（　　）
A．1 B．-1 C．-4 D．-5
组卷：94引用：5难度：0.6
解析
7．已知f（x）=asin2x+bcos2x,其中a,b∈R，ab≠0，若f（x）＜|f（
π
6
）|对x∈R恒成立，且f（
π
2
）＞0，则f（x）的单调递增区间是（　　）
A．[kπ-
π
3
，kπ+
π
6
]（k∈Z） B．[kπ+
π
6
，kπ+
2
π
3
]（k∈Z）
C．[kπ，kπ+
π
2
]（k∈Z） D．[kπ-
π
2
，kπ]（k∈Z）
组卷：142引用：2难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或验算步骤.

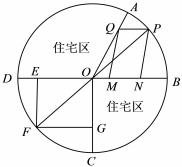21．如图，某圆形小区有两块空余绿化扇形草地AOB（圆心角为
π
3
）和COD（圆心角为
π
2
），BD为圆的直径．现分别要设计出两块社区活动区域，其中一块为矩形区域OEFG，一块为平行四边形区域MNPQ，已知圆的直径PF=2百米，且点P在劣弧AB上（不含端点），点Q在OA上、点G在OC上、点M和N在OB上、点E在OD上，记∠BOP=θ．
（1）经设计，当
OE
-
1
2
MN
达到最大值时，取得最佳观赏效果，求θ取何值时，
OE
-
1
2
MN
最大，最大值是多少？
（2）设矩形OEFG和平行四边形MNPQ面积和为S，求S的最大值及此时cos2θ的值．
组卷：187引用：5难度：0.4
解析
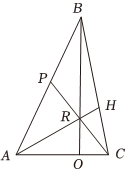22．在△ABC中，P为AB的中点，O在边AC上，BO交CP于R，且|
AO
|=2|
OC
|，设
AB
=
a
，
AC
=
b
．
（1）试用
a
，
b
表示
AR
；
（2）若H在BC上，且RH⊥BC，设|
a
|=2，|
b
|=1，令∠BAC=θ，若θ∈[
π
3
，
2
π
3
]，求
|
CH
|
|
CB
|
的取值范围．
组卷：57引用：1难度：0.5
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

A．充分不必要	B．必要不充分
C．充分必要	D．既不充分也不必要

A．[kπ- π 3 ，kπ+ π 6 ]（k∈Z）	B．[kπ+ π 6 ，kπ+ 2 π 3 ]（k∈Z）
C．[kπ，kπ+ π 2 ]（k∈Z）	D．[kπ- π 2 ，kπ]（k∈Z）

2022-2023学年江苏省苏州中学高一（下）月考数学试卷（3月份）

一、单项选择题：本小题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知平面向量a=（2，4），b=（-3，m+2），a∥b，则m=（ ）

3．已知函数f（x）=sinxcos（2x+φ）（φ∈[0，π]）为偶函数，则φ=（ ）

4．已知a=（-2，-1），b=（λ，1），则λ＞-12是“a与b的夹角为钝角”的（ ）条件

5．若点P（cosα，sinα）在直线y=-2x上，则sin2α+cos（2α+π2）=（ ）

6．如图所示，平面内有三个向量OA，OB，OC，OA与OB的夹角为120°，OA与OC的夹角为150°，且|OA|=|OB|=1，|OC|=33，若OB=λOA+μOC（λ，μ∈R），则λ+μ=（ ）

7．已知f（x）=asin2x+bcos2x,其中a,b∈R，ab≠0，若f（x）＜|f（π6）|对x∈R恒成立，且f（π2）＞0，则f（x）的单调递增区间是（ ）

四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或验算步骤.

22．在△ABC中，P为AB的中点，O在边AC上，BO交CP于R，且|AO|=2|OC|，设AB=a，AC=b．（1）试用a，b表示AR；（2）若H在BC上，且RH⊥BC，设|a|=2，|b|=1，令∠BAC=θ，若θ∈[π3，2π3]，求|CH||CB|的取值范围．

1．已知平面向量
a
=（2，4），
b
=（-3，m+2），
a
∥
b
，则m=（　　）

3．已知函数f（x）=sinxcos（2x+φ）（φ∈[0，π]）为偶函数，则φ=（　　）

4．已知
a
=
（
-
2
，-
1
）
，
b
=
（
λ
，
1
）
，则λ＞-
1
2
是“
a
与
b
的夹角为钝角”的（　　）条件

5．若点P（cosα，sinα）在直线y=-2x上，则sin²α+cos（2α+
π
2
）=（　　）

6．如图所示，平面内有三个向量
OA
，
OB
，
OC
，
OA
与
OB
的夹角为120°，
OA
与
OC
的夹角为150°，且
|
OA
|
=
|
OB
|
=
1
，
|
OC
|
=
3
3
，若
OB
=
λ
OA
+
μ
OC
（λ，μ∈R），则λ+μ=（　　）

7．已知f（x）=asin2x+bcos2x,其中a,b∈R，ab≠0，若f（x）＜|f（
π
6
）|对x∈R恒成立，且f（
π
2
）＞0，则f（x）的单调递增区间是（　　）

22．在△ABC中，P为AB的中点，O在边AC上，BO交CP于R，且|
AO
|=2|
OC
|，设
AB
=
a
，
AC
=
b
．
（1）试用
a
，
b
表示
AR
；
（2）若H在BC上，且RH⊥BC，设|
a
|=2，|
b
|=1，令∠BAC=θ，若θ∈[
π
3
，
2
π
3
]，求
|
CH
|
|
CB
|
的取值范围．