2022-2023学年湖南省湘西州高一（下）期末数学试卷
发布：2024/8/13 0:0:1
一、单项选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。
-
1．已知a,b∈R，a+3i=（b+i）i（i为虚数单位），则（ ）
组卷：2518引用：21难度：0.8 -
2．已知
为不共线的非零向量，a，b，AB=a+5b，BC=-2a+8b，则（ ）CD=3a-3b组卷：2322引用：44难度：0.7 -
3．湘西州有甲草原：龙山县八面山空中草原，乙草原：泸溪县滨江大草原，暑假期间两草原供游客休闲旅游，记事件E=“只去甲草原”，事件 F=“至少去一个草原”，事件 G=“至多去一个草原”，事件H=“不去甲草原”，事件Ⅰ=“一个草原也不去”．下列命题正确的是（ ）
组卷：221引用：6难度：0.9 -
4．已知向量
=（3，4），a=（1，0），b=c+ta，若b，a的夹角与c，b的夹角相等，则t=（ ）c组卷：296引用：3难度：0.7 -
5．已知a,b是两条直线，α，β是两个平面，则下列四个命题正确的有（ ）
①α∥β，a⊂α⇒a∥β；
②α∥β，m⊂α，n⊂β⇒m∥n；
③a⊥b,a⊥α⇒b∥α；
④a⊥α，α∥β，b∥β⇒a⊥b.组卷：183引用：5难度：0.7 -
6．已知圆锥的顶点为P，底面圆心为O，AB为底面直径，∠APB=120°，PA=2，点C在底面圆周上，且二面角P-AC-O 为 45°，则（ ）
组卷：174引用：3难度：0.8 -
7．四名同学各掷骰子5次，分别记录每次骰子出现的点数，根据四名同学的统计结果、可以判断出一定没有出现点数6的是（ ）
组卷：244引用：9难度：0.7
四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.
-
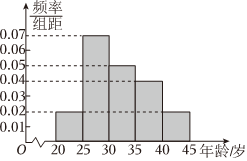21．2022年2月4日，第24届冬季奥林匹克运动会开幕式在北京国家体育场（鸟巢）举行，某调研机构为了了解人们对“奥运会”相关知识的认知程度，针对本市不同年龄和不同职业的人举办了一次“奥运会”知识竞赛，满分100分（95分及以上为认知程度高），结果认知程度高的有m人，按年龄分成5组，其中第一组[20，25），第二组[25，30），第三组[30，35），第四组[35，40），第五组[40，45]，得到如图所示的频率分布直方图，已知第一组有10人．
（1）根据频率分布直方图，估计这m人的平均年龄；
（2）现从以上各组中用分层随机抽样的方法选取20人，担任本市的“奥运会”宣传使者．
（i）若有甲（年龄38），乙（年龄40）两人已确定入选，现计划从第四组和第五组被抽到的使者中，再随机抽取2名作为组长，求甲、乙两人至少有一人被选上的概率；
（ii）若第四组宣传使者的年龄的平均数与方差分别为36和，第五组宣传使者的年龄的平均数与方差分别为42和1，据此估计这m人中35～45岁所有人的年龄的方差．52组卷：169引用：17难度：0.6 -
22．若函数f（x）满足f（x）=f（x+
）且f（3π2+x）=f（π4-x）（x∈R），则称函数f（x）为“M函数”．π4
（1）试判断f（x）=sinx是否为“M函数”，并说明理由；43
（2）函数f（x）为“M函数”，且当x∈[，π]时，f（x）=sinx,求y=f（x）的解析式，并写出在[0，π4]上的单调递增区间；3π2
（3）在（2）的条件下，当x∈[，-π2+π]（k∈N）时，关于x的方程f（x）=a（a为常数）有解，记该方程所有解的和为S（k），求S（3）．3kπ2组卷：245引用：6难度：0.6
