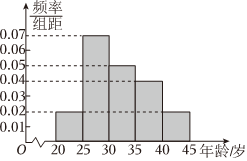
2022年2月4日，第24届冬季奥林匹克运动会开幕式在北京国家体育场（鸟巢）举行，某调研机构为了了解人们对“奥运会”相关知识的认知程度，针对本市不同年龄和不同职业的人举办了一次“奥运会”知识竞赛，满分100分（95分及以上为认知程度高），结果认知程度高的有m人，按年龄分成5组，其中第一组[20，25），第二组[25，30），第三组[30，35），第四组[35，40），第五组[40，45]，得到如图所示的频率分布直方图，已知第一组有10人．
（1）根据频率分布直方图，估计这m人的平均年龄；
（2）现从以上各组中用分层随机抽样的方法选取20人，担任本市的“奥运会”宣传使者．
（i）若有甲（年龄38），乙（年龄40）两人已确定入选，现计划从第四组和第五组被抽到的使者中，再随机抽取2名作为组长，求甲、乙两人至少有一人被选上的概率；
（ii）若第四组宣传使者的年龄的平均数与方差分别为36和52，第五组宣传使者的年龄的平均数与方差分别为42和1，据此估计这m人中35～45岁所有人的年龄的方差．
5
2
【考点】频率分布直方图的应用．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/9 8:0:9组卷：169引用：17难度：0.6
相似题
-
1．如图是一容量为100的样本的重量的频率分布直方图，则由图可估计样本的平均重量为（ ）
发布：2024/12/29 13:30:1组卷：133引用：5难度：0.9 -
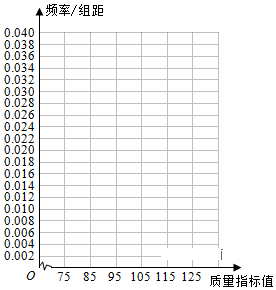2．从某企业生产的产品中抽取100件，测量这些产品的一项质量指标值，由测量结果得如下频数分布表：
（1）在表格中作出这些数据的频率分布直方图；质量指标值分组 [75，85） [85，95） [95，105） [105，115） [115，125） 频数 6 26 38 22 8
（2）估计这种产品质量指标的平均数及方差
（同一组中的数据用该组区间的中点值作代表）；
（3）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定？
附：方差运算公式s2=p1（x1）2+p2（x2-x）2+…+pn（xn-x）2其中pi为第i组频率．-x发布：2024/12/29 13:30:1组卷：116引用：3难度：0.6 -
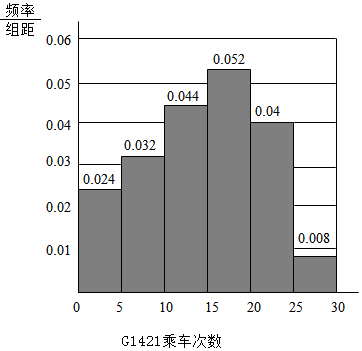3．沪昆高速铁路全线2016年12月28日开通运营．途经鹰潭北站的G1421、G1503两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况，分别在两个车次各随机抽取了100名旅客进行调查，下面是根据调查结果，绘制了月乘车次数的频率分布直方图和频数分布表．
（1）若将频率视为概率，月乘车次数不低于15次的称之为“老乘客”，试问：哪一车次的“老乘客”较多，简要说明理由；G1503乘车次数分组 频数 [0，5） 15 [5，10） 20 [10，15） 25 [15，20） 24 [20，25） 11 [25，0] 5
（2）已知在G1503次列车随机抽到的50岁以上人员有35名，其中有10名是“老乘客”，由条件完成2×2列联表，并根据资料判断，是否有90%的把握认为年龄与乘车次数有关，说明理由．
附：随机变量老乘客 新乘客 合计 50岁以上 50岁以下 合计 （其中n=a+b+c+d为样本容量）k2=n（ad-bc）2（a+b）（c+d）（a+c）（b+d）P（k2≥k0） 0.25 0.15 0.10 0.05 0.025 k0 1.323 2.072 2.706 3.841 5.024 发布：2025/1/9 8:0:2组卷：47引用：2难度：0.7
