高中数学试卷真题_高中数学试卷分析

当前位置：章节挑题

请展开查看知识点列表

人教A版（2019）：选择性必修第一册

教材版本: 人教A版（2019）人教B版（2019）北师大版（2019）苏教版（2019）沪教版（2020）湘教版（2020）鄂教版（2019）人教A版人教B版北师大版苏教版沪教版湘教版大纲版

年级: 必修第一册必修第二册选择性必修第一册选择性必修第二册选择性必修第三册

第一章空间向量与立体几何
第二章直线与圆的方程
第三章圆锥曲线的方程

更多>>

原创

更新中

【优学堂】2026年高考数学一轮复习

明确考点剖析考向配加典例和变式题真题演练及精选模拟全方位助力备考

浏览次数：4354 更新：2025年06月24日

原创

更新中

《黄金讲练》2025-2026学年人教A版（2019）必修第一册高一同步课堂

知识图解新知探究答疑解惑针对训练

浏览次数：843 更新：2025年06月24日

241．A是直线l：y=3x上位于第一象限内的一点，B（3，2）为定点，直线AB交x轴正半轴于点C，求使△AOC面积最小的点A的坐标．
发布：2024/5/23 20:38:36组卷：65引用：2难度：0.5
解析
242．已知点P（3，m）在过M（2，-1）和N（-3，4）两点的直线上，则m的值是
．
发布：2024/5/23 20:38:36组卷：9引用：3难度：0.7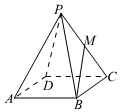
解析
243．如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，侧棱PA的长为1，且PA与AB，AD的夹角都等于60°．若M是PC的中点，则
|
BM
|
=（　　）
A．
3
4
B．
3
4
C．
3
3
D．
3
2
发布：2024/5/23 20:38:36组卷：281引用：4难度：0.7
解析
244．已知直线l₁：x+my=0（m∈R），l₂：mx-y-2m+4=0（m∈R）．
（1）若直线l₁，l₂分别经过定点M，N，求定点M，N的坐标；
（2）是否存在一个定点Q，使得l₁与l₂的交点到定点Q的距离为定值？如果存在，求出定点Q的坐标及定值r；如果不存在，说明理由
发布：2024/5/23 20:38:36组卷：193引用：3难度：0.6
解析
245．已知F₁，F₂是定点，|F₁F₂|=5，若动点P满足|PF₁|+|PF₂|=5，则动点P的轨迹是（　　）
A．直线 B．线段 C．圆 D．椭圆
发布：2024/5/23 20:38:36组卷：117引用：2难度：0.7
解析
246．已知双曲线C的焦点为F₁（-1，0），F₂（1，0），过F₁的直线与双曲线C的左支交于A，B两点，若|AF₁|=2|F₁B|，|AB|=|BF₂|，则C的方程为（　　）
A．
6
x
2
5
-
6
y
2
=
1
B．
7
x
2
3
-
7
y
2
4
=
1
C．
4
x
2
3
-
4
y
2
=
1
D．
5
x
2
3
-
5
y
2
4
=
1
发布：2024/5/23 20:38:36组卷：110引用：4难度：0.7
解析
247．若直线l的方向向量为
v
=（2，1，3），且直线l过A（0，y,3），B（-1，-2，z）两点．则y=
，z=
．
发布：2024/5/23 20:38:36组卷：107引用：2难度：0.9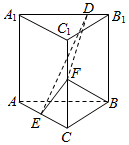
解析
248．已知直三棱柱ABC-A₁B₁C₁中，侧面AA₁B₁B为正方形，AB=BC=2，E，F分别为AC，CC₁的中点，D为棱A₁B₁上的点，BF⊥A₁B₁．
（1）求证：AB⊥BC；
（2）若D为棱A₁B₁的中点，求点A₁到平面DFE的距离；
（3）当B₁D为何值时，平面BB₁C₁C与平面DFE所成二面角（锐角）最小？
发布：2024/5/23 20:38:36组卷：123引用：2难度：0.4
解析
249．已知圆C过点M（0，-2），N（3，1），且圆心C在直线x+2y+1=0上．
（1）求圆C的标准方程；
（2）设直线ax-y+1=0与圆C交于不同的两点A，B，是否存在实数a,使得过点P（2，0）的直线l垂直平分弦AB？若存在，求出实数a的值；若不存在，请说明理由．
发布：2024/5/23 20:38:36组卷：203引用：7难度：0.5
解析
250．已知斜率为
3
的直线l经过抛物线C：y²=2px（p＞0）的焦点F，与抛物线C交于点A，B两点（点A在第一象限），与抛物线的准线交于点D，若|AB|=8，则以下结论正确的是（　　）
A．
1
|
AF
|
+
1
|
BF
|
=
1
B．|AF|=6 C．|BD|=2|BF| D．F为AD中点
发布：2024/5/23 20:38:36组卷：632引用：8难度：0.4
解析

首页上一页 …25 26 27 28 …下一页尾页

A． 6 x 2 5 - 6 y 2 = 1	B． 7 x 2 3 - 7 y 2 4 = 1
C． 4 x 2 3 - 4 y 2 = 1	D． 5 x 2 3 - 5 y 2 4 = 1

241．A是直线l：y=3x上位于第一象限内的一点，B（3，2）为定点，直线AB交x轴正半轴于点C，求使△AOC面积最小的点A的坐标．

242．已知点P（3，m）在过M（2，-1）和N（-3，4）两点的直线上，则m的值是 ．

243．如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，侧棱PA的长为1，且PA与AB，AD的夹角都等于60°．若M是PC的中点，则|BM|=（ ）

245．已知F1，F2是定点，|F1F2|=5，若动点P满足|PF1|+|PF2|=5，则动点P的轨迹是（ ）

246．已知双曲线C的焦点为F1（-1，0），F2（1，0），过F1的直线与双曲线C的左支交于A，B两点，若|AF1|=2|F1B|，|AB|=|BF2|，则C的方程为（ ）

247．若直线l的方向向量为v=（2，1，3），且直线l过A（0，y,3），B（-1，-2，z）两点．则y=，z=．

250．已知斜率为3的直线l经过抛物线C：y2=2px（p＞0）的焦点F，与抛物线C交于点A，B两点（点A在第一象限），与抛物线的准线交于点D，若|AB|=8，则以下结论正确的是（ ）

242．已知点P（3，m）在过M（2，-1）和N（-3，4）两点的直线上，则m的值是
．

243．如图，在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，侧棱PA的长为1，且PA与AB，AD的夹角都等于60°．若M是PC的中点，则
|
BM
|
=（　　）

245．已知F₁，F₂是定点，|F₁F₂|=5，若动点P满足|PF₁|+|PF₂|=5，则动点P的轨迹是（　　）

246．已知双曲线C的焦点为F₁（-1，0），F₂（1，0），过F₁的直线与双曲线C的左支交于A，B两点，若|AF₁|=2|F₁B|，|AB|=|BF₂|，则C的方程为（　　）

247．若直线l的方向向量为
v
=（2，1，3），且直线l过A（0，y,3），B（-1，-2，z）两点．则y=
，z=
．

250．已知斜率为
3
的直线l经过抛物线C：y²=2px（p＞0）的焦点F，与抛物线C交于点A，B两点（点A在第一象限），与抛物线的准线交于点D，若|AB|=8，则以下结论正确的是（　　）