2023年陕西省渭南市赣榆高中高考数学调研试卷（4月份）

一、单项选择题（本大题共8个小题，每小题5分，共40分）

• 1．设集合A={x|x²-3x-4≤0}，B={x|x²+2x＞0，x∈Z}，则A∩B的真子集共有（　　）

  A．15个

  B．16个

  C．31个

  D．32个
  组卷：489引用：12难度：0.7

  解析

• 2．（1-2x）⁵的展开式中，二项式系数最大且系数较大的项的系数为（　　）

  A．40

  B．-40

  C．80

  D．-80
  组卷：103引用：1难度：0.8

  解析

• 3．已知函数f（x）=2sinx+3cosx在x=φ处取得最大值，则cos2φ=（　　）

  A． 3 13 13

  B． 2 13 13

  C． 12 13

  D． 5 13
  组卷：143引用：2难度：0.7

  解析

• 4．酒后驾驶是严重危害交通安全的行为，某交通管理部门对辖区内四个地区（甲、乙、丙、丁）的酒驾治理情况进行检查督导，若“连续8天，每天查获的酒驾人数不超过10”，则认为“该地区酒驾治理达标”，根据连续8天检查所得数据的数字特征推断，酒驾治理一定达标的地区是（　　）

  A．甲地，均值为4，中位数为5

  B．乙地：众数为3，中位数为2

  C．丙地：均值为7，方差为2

  D．丁地：极差为3，75%分位数为8
  组卷：424引用：5难度：0.6

  解析

• 5．随着电商的兴起，物流快递的工作越来越重要了，早在周代，我国便已出现快递制度，据《周礼•秋官》记载，周王朝的官职中设置了主管邮驿，物流的官员“行夫”，其职责要求是“虽道有难，而不时必达”．现某机构对国内排名前五的5家快递公司的某项指标进行了3轮测试（每轮测试的客观条件视为相同），每轮测试结束后都要根据该轮测试的成绩对这5家快递公司进行排名，那么跟测试之前的排名比较，这3轮测试中恰好有1轮测试结果都出现2家公司排名不变的概率为（　　）

  A． 5 72

  B． 5 36

  C． 25 72

  D． 25 36
  组卷：19引用：1难度：0.7

  解析

• 6．已知数列{a_n}满足

  a

  n

  +

  1

  a

  n

  +

  a

  n

  +

  1

  a

  n

  +

  2

  =2，且a₁=1．a₂=

  1

  3

  ，则a₂₀₂₃=（　　）

  A． 1 2021

  B． 1 2022

  C． 1 4045

  D． 1 4044
  组卷：106引用：1难度：0.7

  解析

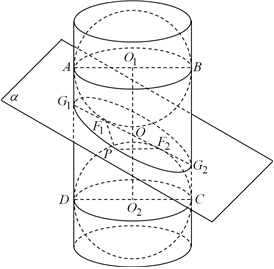• 7．用平面截圆柱面，当圆柱的轴与α所成角为锐角时，圆柱面的截线是一个椭圆．著名数学家Dandelin创立的双球实验证明了上述结论．如图所示，将两个大小相同的球嵌入圆柱内，使它们分别位于α的上方和下方，并且与圆柱面和α均相切．给出下列三个结论：
  ①两个球与α的切点是所得椭圆的两个焦点；
  ②椭圆的短轴长与嵌入圆柱的球的直径相等；
  ③当圆柱的轴与α所成的角由小变大时，所得椭圆的离心率也由小变大．
  其中，所有正确结论的序号是（　　）

  A．①

  B．②③

  C．①②

  D．①③
  组卷：283引用：4难度：0.5

  解析

四、解答题：本题共6小题，共70分。

• 21．在平面直角坐标系xOy中，抛物线C：y²=2x.A₁，A₂为C上两点，且A₁，A₂分别在第一、四象限．直线A₁A₂与x轴正半轴交于A₃，与y负半轴交于A₄．
  （1）若∠A₁OA₂＞90°，求A₃横坐标的取值范围；
  （2）记△A₁OA₂的重心为G，直线A₁A₂，A₃G的斜率分别为k₁，k₂，且k₂=2k₁．若|A₁A₂|=λ|A₃A₄|（λ∈R），证明：λ为定值．
  （3）若过A₁，A₂作抛物线C的切线PA₁，PA₂，交点P在直线x=-1上，求△A₁OA₂面积的最小值．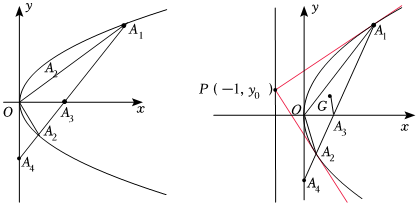
  ​
  组卷：40引用：1难度：0.4

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  x

  e

  x

  和

  g

  （

  x

  ）

  =

  mlnx

  x

  ．
  （1）分别求函数f（x）和g（x）的最大值；
  （2）若m=1，求证：曲线y=f（x）和y=g（x）有唯一公共点P（x₀，y₀），且直线y=y₀与两条曲线y=f（x）和y=g（x）共有三个不同的交点，并探究这三个交点（从左向右）的横坐标是否成等比数列？
  组卷：34引用：1难度：0.2

  解析