2022-2023学年江苏省南京市鼓楼区高二（下）期末数学试卷

一．单项选择题（本题共8小题，每小题5分，共32分，在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．设集合A={-2，-1，0，1，2}，B={x|0≤x＜3}，则A∩B=（　　）

  A．{0，1，2}

  B．{-2，-1，0}

  C．{0，1}

  D．{1，2}
  组卷：96引用：3难度：0.7

  解析

• 2．计算

  A

  2

  8

  的结果是（　　）

  A．10

  B．16

  C．28

  D．56
  组卷：166引用：1难度：0.9

  解析

• 3．一批产品共100件，其中有5件不合格品，从中随机抽取10件产品，则恰有2件不合格品和8件合格品的取法种数是（　　）

  A． C 2 5 C 8 95 C 10 100	B． C 2 5 C 8 95
  C． C 3 5 C 10 95 C 10 100	D． C 3 5 C 10 95
  组卷：74引用：1难度：0.9

  解析

• 4．已知向量

  a

  在向量

  b

  上的投影向量是

  -

  3

  2

  b

  ，且

  b

  =

  （

  1

  ，

  1

  ，-

  1

  ）

  ，则

  a

  •

  b

  =（　　）

  A． - 3 2

  B． 3 2

  C． - 3 2 3

  D． 3 2 3
  组卷：128引用：7难度：0.7

  解析

• 5．函数f（x）=x²在[1，2]上的平均变化率为（　　）

  A．1

  B． 9 4

  C．3

  D．4
  组卷：93引用：1难度：0.8

  解析

• 6．为了考查某种营养液对有机蔬菜的增产效果，某研究所进行试验、获得数据、经过计算后得到K²≈6.795，那么可以认为该营养液为有机蔬菜的增产效果的把握为（　　）
  附：K²临界值表（部分）
  

  P（K2≥k0）	⋯	0.05	0.025	0.010	0.005	0.001	⋯
  k0	⋯	3.841	5.024	6.635	7.879	10.828	⋯

  A．99.9%以上

  B．99.5%以上

  C．99%以上

  D．95%以下
  组卷：87引用：1难度：0.7

  解析

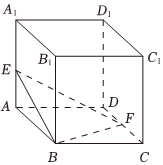• 7．已知平面α与平面β的法向量分别为

  n

  1

  与

  n

  2

  ，平面α与平面β相交，形成四个二面角，约定：在这四个二面角中不大于90°的二面角称为两个平面的夹角，用θ表示这两个平面的夹角，且

  cosθ

  =

  |

  cos

  〈

  n

  1

  ，

  n

  2

  〉

  |

  =

  |

  n

  1

  •

  n

  2

  |

  |

  n

  1

  |

  •

  |

  n

  2

  |

  ，如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，点E为棱AA₁的中点，F为棱CD的中点，则平面BEF与平面BCF的夹角的余弦值为（　　）​

  A． 6 3

  B． 4 21 21

  C． - 6 3

  D． - 4 21 21
  组卷：109引用：1难度：0.6

  解析

四．解答题：本题共6小题，共36分，解答应写出文字说明、证明过程或演算步骤.

• 21．某部门对一种新型产品的效果进行独立重复试验，每次试验结果为成功或不成功，且试验成功的概率为p（0＜p＜1）
  （1）方案一：若试验成功，则试验结束，否则继续试验，且最多试验3次，记X为试验结束时所进行的试验次数，请写出X的分布列，求出E（X）；
  （2）方案二：当实验进行到恰好出现2次成功时结束试验，否则继续试验，已知

  p

  =

  2

  3

  ，求在第n（n≥2）次试验进行完毕时结束试验的概率P（n）；若

  Q

  （

  n

  ）

  =

  P

  （

  n

  ）

  n

  -

  1

  ，当

  n

  ∑

  i

  =

  2

  Q

  （

  i

  ）

  ≥

  3

  5

  时，求n的最小值．
  组卷：110引用：1难度：0.6

  解析

• 22．已知函数f（x）=（1+x）ⁿ
  （1）当n=6时，求在（1+x）ⁿ的展开式中第5项的二项式系数；
  （2）求证：

  C

  0

  n

  -

  C

  1

  n

  2

  +

  C

  2

  n

  3

  +

  ⋯

  +

  （

  -

  1

  ）

  n

  C

  n

  n

  n

  +

  1

  =

  1

  n

  +

  1

  （

  n

  ∈

  N

  *

  ）

  ．
  组卷：81引用：1难度：0.5

  解析