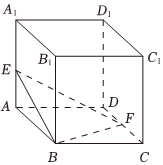
已知平面α与平面β的法向量分别为n1与n2，平面α与平面β相交，形成四个二面角，约定：在这四个二面角中不大于90°的二面角称为两个平面的夹角，用θ表示这两个平面的夹角，且cosθ=|cos〈n1，n2〉|=|n1•n2||n1|•|n2|，如图，在棱长为2的正方体ABCD-A1B1C1D1中，点E为棱AA1的中点，F为棱CD的中点，则平面BEF与平面BCF的夹角的余弦值为（ ）
n
1
n
2
cosθ
=
|
cos
〈
n
1
，
n
2
〉
|
=
|
n
1
•
n
2
|
|
n
1
|
•
|
n
2
|
【考点】空间向量基底表示空间向量．
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/30 8:0:9组卷：109引用：1难度：0.6
相似题
-
1．17世纪，笛卡尔在《几何学》中，通过建立坐标系，引入点的坐标的概念，将代数对象与几何对象建立关系，从而实现了代数问题与几何问题的转化，打开了数学发展的新局面，创立了新分支——解析几何．我们知道，方程x=1在一维空间中表示一个点；在二维空间中，它表示一条直线；在三维空间中，它表示一个平面．那么，过点P0（1，2，1）且以
=（-2，1，3）为法向量的平面的方程为（ ）μ发布：2024/10/23 6:0:3组卷：90引用：4难度：0.8 -
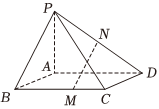2．四棱锥P-ABCD底面ABCD为平行四边形，M，N分别为棱BC，PD上的点，，PN=ND，设CMCB=13，AB=a，AD=b，则向量AP=c用基底MN表示为（ ）{a，b，c}
发布：2024/10/25 4:0:2组卷：434引用：6难度：0.7 -
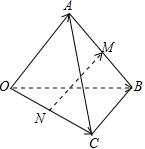3．三棱锥O-ABC中，M，N分别是AB，OC的中点，且=OA，a=OB，b=OC，用c，a，b表示c，则NM等于（ ）NM发布：2024/12/17 2:30:1组卷：2294引用：19难度：0.9
