2023-2024学年山西大学附中高三(上)第二次月考数学试卷(8月份)
发布:2024/9/1 13:0:8
一、选择题:本大题共8小题,每小题5分,共计40分.每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
-
1.设集合A={x|2x+3>0},B={x|x2+4x-5<0},则A∪B=( )
组卷:13引用:3难度:0.9 -
2.某中学举办以“喜迎二十大、永远跟党走,奋进新征程”为主题的演讲比赛,其中9人的比赛成绩依次为:83,85,87,87,88,88,91,93,97(单位:分),则这9人成绩的第80百分位数是( )
组卷:42引用:3难度:0.7 -
3.已知等差数列{an}的前n项和为Sn,若S4=6,S8=18,则S12=( )
组卷:742引用:8难度:0.7 -
4.“白日登山望烽火,黄昏饮马傍交河”是唐代诗人李颀《古从军行》这首诗的开头两句.诗中隐含着一个数学问题——“将军饮马”:即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为x2+y2≤4,若将军从点A(3,1)处出发,河岸线所在直线方程为y=-x-5,并假定将军只要到达军营所在区域即回到军营,那么“将军饮马”的最短总路程为( )
组卷:40引用:5难度:0.7 -
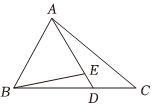 5.如图,在△ABC中,设,AB=a,AC=b,BD=2DC,则AE=4ED=( )BE组卷:905引用:28难度:0.7
5.如图,在△ABC中,设,AB=a,AC=b,BD=2DC,则AE=4ED=( )BE组卷:905引用:28难度:0.7 -
6.对于函数y=f(x),若存在f(x0)=-f(-x0),则称点(x0,f(x0))与点(-x0,f(-x0))是函数的一对“隐对称点”.若m>0时,函数
的图象上恰有2对“隐对称点”,则实数m的取值范围为( )f(x)=lnx,x>0-mx2-mx,x≤0组卷:49引用:1难度:0.3 -
7.已知P(2,4)是抛物线C:y2=2px(p>0)上一点,过C的焦点F的直线l与C交于A,B两点,则|AF|+9|BF|的最小值为( )
组卷:232引用:3难度:0.5
四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.某校20名学生的数学成绩xi(i=1,2,⋯,20)和知识竞赛成绩yi(i=1,2,⋯,20)如下表:
计算可得数学成绩的平均值是学生编号i 1 2 3 4 5 6 7 8 9 10 数学成绩xi 100 99 96 93 90 88 85 83 80 77 知识竞赛成绩yi 290 160 220 200 65 70 90 100 60 270 学生编号i 11 12 13 14 15 16 17 18 19 20 数学成绩xi 75 74 72 70 68 66 60 50 39 35 知识竞赛成绩yi 45 35 40 50 25 30 20 15 10 5 ,知识竞赛成绩的平均值是x=75,并且y=90,20∑i=1(xi-x)2=6464,20∑i=1(yi-y)2=149450.20∑i=1(xi-x)(yi-y)=21650
(1)求这组学生的数学成绩和知识竞赛成绩的样本相关系数(精确到0.01).
(2)设N∈N*,变量x和变量y的一组样本数据为{(xi,yi)|i=1,2,⋯,N},其中xi(i=1,2,⋯,N)两两不相同,yi(i=1,2,⋯,N)两两不相同.记xi在{xn|n=1,2,⋯,N}中的排名是第Ri位,yi在{yn|n=1,2,⋯,N}中的排名是第Si位,i=1,2,⋯,N.定义变量x和变量y的“斯皮尔曼相关系数”(记为ρ)为变量x的排名和变量y的排名的样本相关系数.
(i)记di=Ri-Si,i=1,2,⋯,N.证明:.ρ=1-6N(N2-1)N∑i=1d2i
(ii)用(i)的公式求这组学生的数学成绩和知识竞赛成绩的“斯皮尔曼相关系数”(精确到0.01).
(3)比较(1)和(2)(ii)的计算结果,简述“斯皮尔曼相关系数”在分析线性相关性时的优势.
注:参考公式与参考数据.;r=n∑i=1(xi-x)(yi-y)n∑i=1(xi-x)2n∑i=1(yi-y)2;n∑k=1k2=n(n+1)(2n+1)6.6464×149450≈31000组卷:217引用:4难度:0.3 -
22.双曲线
的左、右焦点分别是F1,F2,离心率为3,点x2a2-y2b2=1(a>0,b>0)在双曲线上.(324,1)
(1)求双曲线的标准方程;
(2)A,B分别为双曲线的左,右顶点,若点P为直线上一点,直线PA与双曲线交于另一点M,直线PB与双曲线交于另一点N,求直线MN恒经过的定点坐标.x=13组卷:256引用:4难度:0.4


