2023-2024学年上海交大附中高三（上）摸底数学试卷

一、填空题.（本题共12小题，前6题每小题4分；后6题每小题4分，共54分.请在横线上方填写最终的、最简、完整的结果）

• 1．已知集合A={1，2，3，4，5}，B={x|x=2t+1，t∈A}，则A∩B=

  ．
  组卷：79引用：4难度：0.8

  解析

• 2．不等式|x+1|+|x-3|≤6的解集为

  ．
  组卷：207引用：4难度：0.5

  解析

• 3．已知点A（-2，3），B（1，-1），则

  OA

  在

  OB

  方向上的数量投影为

  ．
  组卷：50引用：2难度：0.7

  解析

• 4．已知z=3+4i,若实数a、b满足z+a

  z

  +b|z|=0，则a+b=

  ．
  组卷：36引用：2难度：0.8

  解析

• 5．如图△ABC中，

  ∠

  ACB

  =

  90

  °

  ，

  ∠

  ABC

  =

  30

  °

  ，

  BC

  =

  5

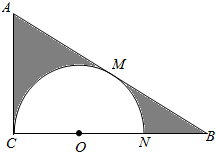  ，在三角形内挖去一个半圆（圆心O在边BC上，半圆与AC、AB分别相切于点C，M，交BC于点N），则图中阴影部分绕直线BC旋转一周所得旋转体的体积为

  ．
  组卷：44引用：8难度：0.6

  解析

• 6．设x、y均为正数，且xy=1，则5^x•5^y的最小值为

  ．
  组卷：72引用：4难度：0.8

  解析

• 7．一个小球作简谐振动，其运动方程为

  x

  （

  t

  ）

  =

  2

  sin

  （

  πt

  +

  π

  3

  ）

  ，其中x（t）（单位：cm）是小球相对于平衡点的位移，t（单位：s）为运动时间，则小球在t=2时的瞬时速度为

  cm/s.
  组卷：115引用：4难度：0.8

  解析

三、解答题.（本大题共5小题，满分78分.请写出必要的证明过程或演算步骤）

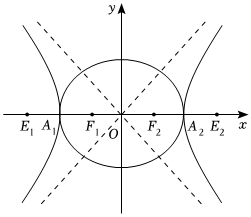• 20．如图，椭圆Γ₁、双曲线Γ₂中都是坐标原点O，焦点都在x轴上，且具有相同的顶点A₁、A₂，Γ₁的焦点为F₁、F₂，Γ₂的焦点为E₁、E₂，点A₁、F₁、O、F₂、A₂恰为线段E₁E₂的六等分点，我们把Γ₁与Γ₂合成为曲线Γ，已知Γ₁的长轴长为4．
  （1）求曲线Γ₁与Γ₂的方程；
  （2）若M是Γ上的一动点，T（0，4）为定点，求|MT|的最小值；
  （3）若直线l过点O，与Γ₁交于P₁、P₂两点，与Γ₂交于Q₁、Q₂两点，点P₁、Q₁位于同一象限，且直线P₁F₁∥Q₁E₁，求直线l的斜率．
  组卷：40引用：2难度：0.5

  解析

• 21．记f'（x），g′（x）分别为函数f（x），g（x）的导函数．若存在实数x₀，满足f（x₀）=g（x₀）且f'（x₀）=g′（x₀），则称x₀为函数f（x）与g（x）的一个“S点”．
  （1）证明：函数f（x）=x与g（x）=x²+2x-2不存在“S点”；
  （2）若存在实数b,使得函数f（x）=ax²+b与g（x）=lnx存在“S点”，求实数a的取值范围；
  （3）已知函数f（x）=-x²+a,

  g

  （

  x

  ）

  =

  b

  e

  x

  x

  ．对任意常数a＞0，判断是否存在常数b＞0，使函数f（x）与g（x）在区间（0，+∞）内存在“S点”，并说明理由．
  组卷：45引用：2难度：0.4

  解析