2022-2023学年黑龙江省鹤岗一中高一(下)期末数学试卷
发布:2024/6/17 8:0:9
一、单选题:本大题共8道小题,每个小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1.若z•i=2+3i(i是虚数单位),则在复平面内z对应的点位于( )
组卷:26引用:4难度:0.7 -
2.在△ABC中,若AB=4,BC=5,AC=6,则
=( )AB•BC组卷:152引用:8难度:0.7 -
3.下列结论中正确是( )
组卷:152引用:5难度:0.7 -
4.已知向量
,a=(-3,4),b=(2,-2),若c=(5,-1)与a垂直,则实数λ的值为( )λb+c组卷:72引用:3难度:0.7 -
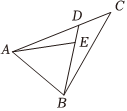 5.如图,点D为△ABC的边AC上靠近点C的三等分点,,设DE=14DB,AB=a,则AC=b=( )AE组卷:318引用:7难度:0.7
5.如图,点D为△ABC的边AC上靠近点C的三等分点,,设DE=14DB,AB=a,则AC=b=( )AE组卷:318引用:7难度:0.7 -
6.在三棱锥P-ABC中,PA⊥底面ABC,AB=2,AC=AP,BC⊥CA,若三棱锥P-ABC外接球的表面积为5π,则BC=( )
组卷:234引用:9难度:0.5 -
 7.如图,生活中有很多球缺状的建筑.球被平面截下的部分叫做球缺,截面叫做球缺的底面,球缺的曲面部分叫做球冠,垂直于截面的直径被截后的线段叫做球缺的高.球冠面积公式为S=2πRH,球缺的体积公式为,其中R为球的半径,H为球缺的高.现有一个球被一平面所截形成两个球缺,若两个球冠的面积之比为1:2,则这两个球缺的体积之比为( )V=13π(3R-H)H2组卷:223引用:8难度:0.6
7.如图,生活中有很多球缺状的建筑.球被平面截下的部分叫做球缺,截面叫做球缺的底面,球缺的曲面部分叫做球冠,垂直于截面的直径被截后的线段叫做球缺的高.球冠面积公式为S=2πRH,球缺的体积公式为,其中R为球的半径,H为球缺的高.现有一个球被一平面所截形成两个球缺,若两个球冠的面积之比为1:2,则这两个球缺的体积之比为( )V=13π(3R-H)H2组卷:223引用:8难度:0.6
四、解答题:本大题共6道小题,共70分。解答应写出文字说明、证明过程或演算步骤。
-
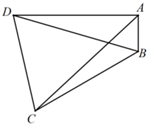 21.由于某地连晴高温,森林防灭火形势严峻,某部门安排了甲、乙两名森林防火护林员对该区域开展巡查.现甲、乙两名森林防火护林员同时从A地出发,乙沿着正西方向巡视走了3km后到达D点,甲向正南方向巡视若干公里后到达B点,又沿着南偏西60°的方向巡视走到了C点,经过测量发现∠ACD=60°.设∠ACB=θ,如图所示.
21.由于某地连晴高温,森林防灭火形势严峻,某部门安排了甲、乙两名森林防火护林员对该区域开展巡查.现甲、乙两名森林防火护林员同时从A地出发,乙沿着正西方向巡视走了3km后到达D点,甲向正南方向巡视若干公里后到达B点,又沿着南偏西60°的方向巡视走到了C点,经过测量发现∠ACD=60°.设∠ACB=θ,如图所示.
(1)设甲护林员巡视走过的路程为S=AB+BC,请用θ表示S,并求S的最大值;
(2)为了强化应急应战准备工作,有关部门决定在△BCD区域范围内储备应急物资,求△BCD区域面积的最大值.组卷:43引用:6难度:0.6 -
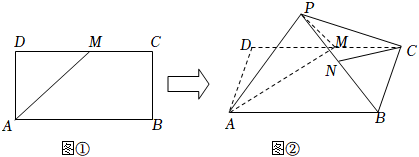
22.如图①所示,长方形ABCD中,AD=1,AB=2,点M是边CD的中点,将△ADM沿AM翻折到△PAM,连结PB,PC,得到图②的四棱锥P-ABCM.
(1)求四棱锥P-ABCM的体积的最大值;
(2)若棱PB的中点为N,求CN的长;
(3)设P-AM-D的大小为θ,若,求平面PAM和平面PBC夹角余弦值的最小值.θ∈(0,π2]组卷:709引用:18难度:0.3


