2023-2024学年江苏省南京九中高三（上）学情检测数学试卷（10月份）
发布：2024/9/10 9:0:8
一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
-
1．已知a,b∈R，复数z=a-bi,则|z|2=（ ）
组卷：55引用：4难度：0.8 -
2．已知向量
，a=（2，0），若b=（sinα，32）在b上的投影向量a，则sinα为（ ）c=（12，0）组卷：39引用：1难度：0.8 -
3．已知非负实数x,y满足
，则x+y的最小值为（ ）13x+y+12y+2=1组卷：128引用：2难度：0.7 -
4．过点A（1，1），B（3，3）且圆心在直线y=3x上的圆与y轴相交于P，Q两点，则|PQ|=（ ）
组卷：178引用：6难度：0.6 -
5．中国空间站（天宫空间站，英文名称ChinaSpaceStation）是中华人民共和国建设中的‘个空间站系统，预计在2022年前后建成．空间站轨道高度为400～500公里，倾角42～43度，设计寿命为10年，长期驻留3人，总重量可达180吨，以进行较大规模的空间应用．某项实验在空间站进行，实验开始时，某物质的含量为1.2mg/cm3，每经过1小时，该物质的含量都会减少20%，若该物质的含量不超过0.2mg/cm3，则实验进入第二阶段，那么实验进入第二阶段至少需要多少小时？（ ）（需要的小时数取整数，参考数据：lg2≈0.30，lg3≈0.48）
组卷：5引用：4难度：0.6 -
6．在{1，2，⋯，12}的非空真子集中，满足最大元素与最小元素之和为13的集合个数为（ ）
组卷：45引用：1难度：0.6 -
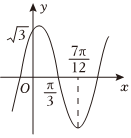7．如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜）的图象的一部分，则要得到该函数的图象，只需要将函数g（x）=1-2π2sinxcosx-2sin2x的图象（ ）3组卷：159引用：3难度：0.6
四、解答题（本题含6小题，其中第17题10分，其它均12分，共70分．解答应写出文字说明，证明过程或演算步骤）
-
21．体检时，为了确定体检人是否患有某种疾病，需要对其血液采样进行化验，若结果呈阳性，则患有该疾病；若结果呈阴性，则未患有该疾病．对于n（n∈N*）份血液样本，有以下两种检验方式：一是逐份检验，则需检验n次．二是混合检验，将n份血液样本分别取样混合在一起，若检验结果为阴性，那么这n份血液全为阴性，因而检验一次就够了；如果检验结果为阳性，为了明确这n份血液究竟哪些为阳性，就需要对它们再次取样逐份检验，则n份血液检验的次数共为n+1次．已知每位体检人未患有该疾病的概率为
，而且各体检人是否患该疾病相互独立．3p（0＜p＜1）
（1）若，求3位体检人的血液样本混合检验结果为阳性的概率；p=89
（2）某定点医院现取得6位体检人的血液样本，考虑以下两种检验方案：
方案一：采用混合检验；
方案二：平均分成两组，每组3位体检人血液样本采用混合检验．
若检验次数的期望值越小，则方案越“优”．试问方案一、二哪个更“优”？请说明理由．组卷：174引用：3难度：0.5 -
22．定义：若无穷数列{an}满足{an+1-an}是公比为q的等比数列，则称数列{an}为“M（q）数列”．设数列{bn}中，b1=1，b3=7．
（1）若b2=4，且数列{bn}为“M（q）数列”，求数列{bn}的通项公式：
（2）设数列{bn}的前n项和为Sn，且，请判断数列{bn}是否为“M（q）数列”，并说明理由；bn+1=2Sn-12n+λ
（3）若数列{bn}是“M（2）数列”，是否存在正整数m,n,使得？若存在，请求出所有满足条件的正整数m,n；若不存在，请说明理由．40412020＜bmbn＜40422020组卷：103引用：3难度：0.5
