当前位置：试卷中心 > 试卷详情

2023-2024学年福建省厦门一中高二（上）月考数学试卷（10月份）

发布：2024/9/14 11:0:13

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．过点P（1，1）且方向向量为（-1，3）的直线方程为（　　）
A．3x+y+4=0 B．3x+y-4=0 C．3x-y+2=0 D．3x-y-2=0
组卷：801引用：5难度：0.8
解析
2．已知直线l₁：mx+y=0与直线l₂：9x+my-10=0平行，则实数m的值为（　　）
A．-3 B．3 C．±3 D．0
组卷：66引用：5难度：0.8
解析
3．在正三棱柱ABC-A₁B₁C₁中，AA₁=AB，点M、N分别为棱A₁C₁、A₁B₁的中点，则AM和BN所成角的余弦值为（　　）
A．
7
10
B．
15
10
C．
85
10
D．
-
7
10
组卷：115引用：4难度：0.8
解析
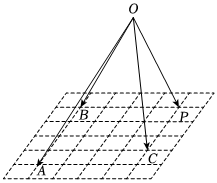4．如图，平面ABC内的小方格均为正方形，点P为平面ABC内的一点，O为平面ABC外一点，设
OP
=
m
OA
+
n
OB
+
2
OC
，则m+n的值为（　　）
A．1 B．-1 C．2 D．-2
组卷：78引用：2难度：0.5
解析
5．已知三条直线l₁，l₂，l₃的斜率分别为k₁，k₂，k₃，倾斜角分别为α，β，γ．若α＜β＜γ，则下列关系不可能成立的是（　　）
A．k₃＜k₁＜k₂ B．k₁＜k₂＜k₃ C．k₂＜k₃＜k₁ D．k₃＜k₂＜k₁
组卷：388引用：4难度：0.7
解析
6．空间直角坐标系中，A（0，0，0）、B（1，1，1）、C（1，0，0））、D（-1，2，1），其中A∈α，B∈α，C∈β，D∈β，已知平面α∥平面β，则平面α与平面β间的距离为（　　）
A．
26
26
B．
13
13
C．
3
3
D．
5
5
组卷：160引用：2难度：0.6
解析
7．阅读材料：空间直角坐标系O-xyz中，过点P（x₀，y₀，z₀）且一个法向量为
n
=
（
a
,
b
,
c
）
的平面α的方程为a（x-x₀）+b（y-y₀）+c（z-z₀）=0；过点P（x₀，y₀，z₀）且一个方向向量为
d
=
（
u
,
v
,
w
）
（
uvw
≠
0
）
的直线l的方程为
x
-
x
0
u
=
y
-
y
0
v
=
z
-
z
0
w
．利用上面的材料，解决下面的问题：已知平面α的方程为3x-5y+z-7=0，直线l是平面x-3y+7=0与4y+2z+1=0的交线，则直线l与平面α所成角的正弦值为（　　）
A．
10
35
B．
7
5
C．
7
15
D．
31
7735
7735
组卷：45引用：3难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

21．如图①所示，长方形ABCD中，AD=1，AB=2，点M是边CD的中点，将△ADM沿AM翻折到△PAM，连接PB，PC，得到图②的四棱锥P-ABCM．

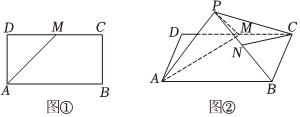
（1）求四棱锥P-ABCM的体积的最大值；
（2）设P-AM-D的大小为θ，若
θ
∈
（
0
，
π
2
]
，求平面PAM和平面PBC夹角余弦值的最小值．
组卷：53引用：1难度：0.4
解析
22．已知直线l：ax+by+c=0和点P（x₀，y₀），点P到直线l的有向距离d（P，l）用如下方法规定：若b≠0，
d
（
P
，
l
）
=
|
b
|
|
a
x
0
+
b
y
0
+
c
|
b
a
2
+
b
2
，若b=0，
d
（
P
，
l
）
=
a
x
0
+
c
a
．
（1）已知直线l₁：3x-4y+12=0，直线l₂：2x+3=0，求原点O到直线l₁，l₂的有向距离d（O，l₁），d（O，l₂）；
（2）已知点A（2，1）和点B（3，-1），是否存在通过点A的直线l₃，使得d（B，l₃）=2？如果存在，求出所有这样的直线l₃，如果不存在，说明理由；
（3）设直线l₄：xcosα+2ysinα-2=0，问是否存在实数t＞0，使得对任意的参数α都有：点F₁（-t,0），F₂（t,0）到l₄的有向距离d（F₁，l₄），d（F₂，l₄）满足d（F₁，l₄）•d（F₂，l₄）=1？如果满足，求出所有满足条件的实数t；如果不存在，请说明理由．
组卷：140引用：6难度：0.5
解析