当前位置：试卷中心 > 试卷详情

2023-2024学年广东省河源市联考高三（上）开学数学试卷

发布：2024/8/2 8:0:9

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．若复数z的虚部小于0，且z²=-1，则z（1-z）=（　　）
A．1+i B．1-i C．-1+i D．-1-i
组卷：14引用：6难度：0.8
解析
2．已知集合M={x∈Z|y=ln（1-x²）}，N={-1，0，1}，则M∩N=（　　）
A．{0} B．{-1，1} C．{-1，0，1} D．∅
组卷：14引用：2难度：0.9
解析
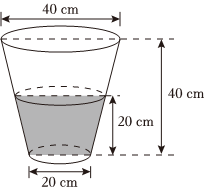3．最早的测雨器记载见于南宋数学家秦九韶所著的《数书九章》（1247年）．该书第二章为“天时类”，收录了有关降水量计算的四个例子，分别是“天池测雨”、“圆罂测雨”、“峻积验雪”和“竹器验雪”．如图“竹器验雪”法是下雪时用一个圆台形的器皿收集雪量（平地降雪厚度=器皿中积雪体积除以器皿口面积），已知数据如图（注意：单位cm），则平地降雪厚度的近似值为（　　）
A．
91
12
cm
B．
31
4
cm
C．
95
12
cm
D．
97
12
cm
组卷：331引用：9难度：0.6
解析
4．已知公差不为零的等差数列{a_n}的前n项和为S_n，a₆=2a₃，则
S
17
a
3
=（　　）
A．17 B．34 C．48 D．51
组卷：115引用：2难度：0.7
解析
5．已知
a
lo
g
3
a
=
3
lo
g
3
81
，则a=（　　）
A．9或
1
3
B．81或
1
3
C．9或
1
9
D．81或
1
81
组卷：162引用：1难度：0.8
解析
6．已知
f
（
x
）
=
sin
（
π
2
x
+
φ
）
（
φ
∈
[
0
，
π
）
）
在
（
-
1
6
，
1
6
）
上单调递减，且
f
（
0
）
=
1
2
，则（　　）
A．
φ
=
π
6
B．
φ
=
π
3
C．
φ
=
2
π
3
D．
φ
=
5
π
6
组卷：70引用：1难度：0.7
解析
7．已知直线
x
-
y
+
1
4
=
0
与抛物线y=x²相交于A，B两点，过线段AB的中点P作一条垂直于x轴的直线m与直线l：
y
=
-
1
4
交于点Q，则△QAB的面积为（　　）
A．
1
4
B．
2
2
C．1 D．
2
组卷：40引用：1难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出必要的文字说明，证明过程或演算步骤.

21．某学校组织一项竞赛，在初赛中有两轮答题：第一轮从A类的三个问题中随机选两题作答，每答对一题得20分，答错得0分；第二轮从B类的分值分别为20，30，40的3个问题中随机选两题作答，每答对一题得满分，答错得0分．若两轮总积分不低于90分，则晋级复赛．甲、乙同时参赛，在A类的三个问题中，甲每个问题答对的概率均为
1
2
，乙只能答对两个问题；在B类的3个分值分别为20，30，40的问题中，甲答对的概率分别为1，
2
3
，
1
3
，乙答对的概率分别为
3
4
，
1
2
，
1
4
．甲、乙回答任一问题正确与否互不影响．设甲、乙在第一轮的得分分别为X，Y．
（1）分别求X，Y的概率分布列；
（2）分别计算甲、乙晋级复赛的概率，并请说明谁更容易晋级复赛？
组卷：80引用：3难度：0.5
解析
22．已知函数f（x）=ln（x+1），g（x）=f（x）+ae^x，其中a∈R．
（1）求过点（-1，-1）且与函数f（x）的图象相切的直线方程；
（2）①求证：当x＞0时，
e
x
＞
1
+
x
+
x
2
2
；
②若函数g（x）有两个不同的零点x₁，x₂，求证：
|
x
2
-
x
1
|
＜
2
1
a
2
+
2
a
-
1
．
组卷：122引用：3难度：0.1
解析