2023-2024学年山东省青岛市市南区超银中学八年级（上）奇点计划选拔数学试卷

一、选择题（每题3分，共24分）

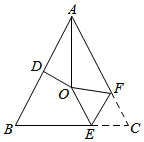• 1．如图，在△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，有如下五个结论：①AO⊥BC；②OD=OE；③△OEF是等边三角形；④△OEF≌△CEF；⑤∠OEF=54°．则上列说法中正确的个数是（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：515引用：8难度：0.6

  解析

• 2．对于实数a、b,定义符号min{a,b}为：当a≥b时，min{a,b}=b；当a＜b时，min{a,b}=a.例如：min{2，-1}=-1，若关于x的函数y=min{2x-1，-x+3}，则该函数的最大值是（　　）

  A．1

  B． 4 3

  C． 5 3

  D．2
  组卷：272引用：3难度：0.6

  解析

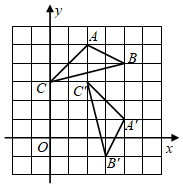• 3．如图，将△ABC绕点P顺时针旋转得到△A'B'C'，则点P的坐标为（　　）

  A．（1，1）

  B．（1，2）

  C．（1，3）

  D．（1，4）
  组卷：965引用：12难度：0.6

  解析

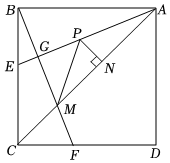• 4．如图，正方形ABCD的边长为6，点E，F分别为边BC，CD上两点，CF=BE，AE平分∠BAC，连接BF，分别交AE，AC于点G，M，点P是线段AG上的一个动点，过点P作PN⊥AC，垂足为N，连接PM，则下列结论正确的个数是（　　）
  ①△ABE≌△BCF；
  ②

  AM

  =

  4

  2

  ；
  ③PM+PN的最小值为

  3

  2

  ；
  ④三角形AGM的面积是

  3

  2

  +

  1

  ．

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：112引用：1难度：0.5

  解析

• 5．数论是研究整数性质的一门理论．它渗透于我们的中小学数学教材之中，其中整数的奇偶性也属于数论研究内容的一部分，偶数与奇数的运算性质为：奇数±奇数=偶数；偶数±偶数=偶数；奇数±偶数=奇数；奇数×奇数=奇数；偶数×偶数=偶数；奇数×偶数=偶数．有这样一道关于整式运算的试题：已知a,b,c为自然数，使得（a^b-b^c）（b^c-c^a）（c^a-a^b）=11713，请求出a,b,c的值．小明运用整数的奇偶性进行分析，得出以下结论：
  ①要使等式成立，则（a^b-b^c），（b^c-c^a），（c^a-a^b）三个因式均为奇数；
  ②可以求出a,b,c的1组解；
  ③可以求出a,b,c的6组解；
  ④没有符合条件的自然数a,b,c.
  以上结论正确的个数为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：148引用：2难度：0.5

  解析

• 6．化简

  1

  8

  +

  11

  +

  1

  11

  +

  14

  +

  1

  14

  +

  17

  +

  1

  17

  +

  20

  +

  1

  20

  +

  23

  +

  1

  23

  +

  26

  +

  1

  26

  +

  29

  +

  1

  29

  +

  32

  的结果是（　　）

  A．1

  B． 2 2 3

  C． 2 2

  D． 4 2
  组卷：817引用：3难度：0.9

  解析

• 7．10个人围成一圈做游戏．游戏的规则是：每个人心里都想一个数，并把自己想的数告诉与他相邻的两个人，然后每个人将与他相邻的两个人告诉他的数的平均数报出来，若报出来的数如图所示，则报出来的数是3的人心里想的数是（　　）

  A．2

  B．-2

  C．4

  D．-4
  组卷：1275引用：12难度：0.3

  解析

• 8．已知关于x,y的方程组

  x - 3 y = 4 - t

  x + y = 3 t

  ，其中-3≤t≤1，给出下列结论：
  ①

  x = 1

  y = - 1

  是方程组的解；
  ②若x-y=3，则t=-2；
  ③若M=2x-y-t,则M的最小值为-3；
  ④若y≥-1时，则0≤x≤3；
  其中正确的有（　　）

  A．①②

  B．①③

  C．①②③

  D．①③④
  组卷：1165引用：5难度：0.4

  解析

三、解答题（每题8分，共40分）

• 24．《见微知著》读到：从一个简单的经典问题出发，从特殊到一般，由简单到复杂：从部分到整体，由低维到高维，知识与方法上的类比是探索发展重要途径，是思想阀门发现新问题、结论的重要方法．
  阅读材料一：利用整体思想解题，运用代数式的恒等变形，使不少依照常规思路难以解决的问题找到简便解决方法，常用的途径有：（1）整体观察；（2）整体设元；（3）整体代入；（4）整体求和等．
  例如：ab=1，求证：

  1

  1

  +

  a

  +

  1

  1

  +

  b

  =

  1

  
  证明：左边=

  1

  1

  +

  a

  +

  1

  1

  +

  b

  =

  ab

  ab

  +

  a

  +

  1

  1

  +

  b

  =

  b

  1

  +

  b

  +

  1

  1

  +

  b

  =

  1

  
  波利亚在《怎样解题》中指出：“当你找到第一个藤菇或作出第一个发现后，再四处看看，他们总是成群生长”类似问题，我们有更多的式子满足以上特征：
  阅读材料二
  基本不等式

  a

  +

  b

  2

  ≥

  ab

  （a＞0，b＞0），当且仅当a=b时等号成立，它是解决最值问题的有力工具．
  例如：在x＞0的条件下，当x为何值时，

  x

  +

  1

  x

  有最小值，最小值是多少？
  解：∵x＞0，

  1

  x

  ＞

  0

  ，∴

  x

  +

  1

  x

  2

  ≥

  x

  ⋅

  1

  x

  =

  1

  =

  1

  ，即

  x

  +

  1

  x

  ≥

  2

  ，
  当且仅当

  x

  =

  1

  x

  ，即x=1时，

  x

  +

  1

  x

  有最小值，最小值为2，
  请根据阅读材料解答下列问题：
  （1）已知ab=1，求下列各式的值：
  ①

  1

  1

  +

  a

  2

  +

  1

  1

  +

  b

  2

  =

  ；
  ②

  1

  1

  +

  a

  n

  +

  1

  1

  +

  b

  n

  =

  ；
  （2）若abc=1，求

  5

  a

  ab

  +

  a

  +

  1

  +

  5

  b

  bc

  +

  b

  +

  1

  +

  5

  c

  ca

  +

  c

  +

  1

  的值；
  （3）已知长方形的面积为9，求此长方形周长的最小值；
  （4）若正数a、b满足ab=1，求

  M

  =

  1

  1

  +

  a

  +

  1

  1

  +

  2

  b

  的最小值．
  组卷：693引用：2难度：0.3

  解析

• 25．问题提出
  （1）如图①，在Rt△ABC中，∠B=90°，AB=3，BC=4．若点P是边AC上一点，则BP的最小值为

  ；
  问题探究
  （2）如图②，在Rt△ABC中，∠B=90°，AB=BC=2，点E是BC的中点．若点P是边AC上一点，试求PB+PE的最小值；
  问题解决
  （3）某市一湿地公园内有一条四边形ABCD型环湖路，如图③所示．已知AD=2000米，CD=1000米，∠A=60°，∠B=90°，∠C=150°．为了进一步提升服务休闲功能，满足市民游园和健身需求，现要修一条由CE，EF，FC连接而成的步行景观道，其中，点E，F分别在边AB，AD上．为了节省成本，要使所修的这条步行景观道最短，即CE+EF+FC的值最小，求此时BE，DF的长．（路面宽度忽略不计）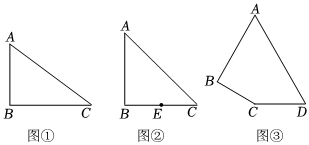
  
  组卷：1797引用：6难度：0.1

  解析