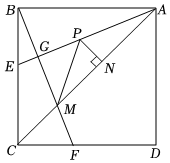
如图，正方形ABCD的边长为6，点E，F分别为边BC，CD上两点，CF=BE，AE平分∠BAC，连接BF，分别交AE，AC于点G，M，点P是线段AG上的一个动点，过点P作PN⊥AC，垂足为N，连接PM，则下列结论正确的个数是（ ）
①△ABE≌△BCF；
②AM=42；
③PM+PN的最小值为32；
④三角形AGM的面积是32+1．
AM
=
4
2
3
2
3
2
+
1
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/20 1:0:1组卷：113引用：1难度：0.5
相似题
-
1．如图，正方形ABCD的边长为6，∠DAC的平分线交DC于点E．若点P，Q分别是AD和AE上的动点，则DQ+PQ的最小值是 ．发布：2025/5/23 2:30:1组卷：480引用：1难度：0.5 -
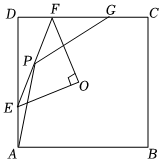2．如图，在边长为8的正方形ABCD中，点O为正方形的中心，点E为AD边上的动点，连接OE，作OF⊥OE交CD于点F，连接EF，P为EF的中点，G为边CD上一点，且CD=4CG，连接PA，PG，则PA+PG的最小值为 ．发布：2025/5/23 6:30:1组卷：612引用：7难度：0.2 -
3．如图，已知在平面直角坐标系中，点B的坐标是（0，4），∠OBA=60°，点A在x轴正半轴上．将Rt△ABO中沿着直线AB平移得到Rt△A'B'O'，当OB'+OA'最小时，Rt△ABO和Rt△A'B'O'的重叠部分面积是 ．发布：2025/5/22 23:0:1组卷：304引用：1难度：0.6
