 如图甲所示,两平行金属板水平放置,间距为d,金属板长为2d,两金属板间加如图乙所示的电压(初始时上金属板带正电),其中U0=16md2qT2。一粒子源连续均匀发射质量为m、电荷量为+q的带电粒子(初速度v0=4dT,重力忽略不计),该粒子源射出的带电粒子恰好从上金属板左端的下边缘水平进入两金属板间。(若粒子碰到两金属板即被金属板吸收),求:
如图甲所示,两平行金属板水平放置,间距为d,金属板长为2d,两金属板间加如图乙所示的电压(初始时上金属板带正电),其中U0=16md2qT2。一粒子源连续均匀发射质量为m、电荷量为+q的带电粒子(初速度v0=4dT,重力忽略不计),该粒子源射出的带电粒子恰好从上金属板左端的下边缘水平进入两金属板间。(若粒子碰到两金属板即被金属板吸收),求:
(1)能从板间飞出的粒子在板间运动的时间;
(2)若t=T4时刻进入两极板之间,飞出极板时的偏移量y是多少;
(3)能从板间飞出的粒子数占入射粒子数的百分比。
U
0
=
16
m
d
2
q
T
2
v
0
=
4
d
T
t
=
T
4
【考点】从能量转化与守恒的角度解决电场中的问题.
【答案】(1)能从板间飞出的粒子在板间运动的时间为;
(2)飞出极板时的偏移量y是d;
(3)在(其中n=0,1,2,3……) 时刻进入两金属板间的带电粒子不碰到金属板而能够飞出两金属板间。
T
2
(2)飞出极板时的偏移量y是d;
(3)在
(
1
4
+
n
)
T
≤
t
≤
(
2
4
+
n
)
T
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/12 0:0:8组卷:26引用:4难度:0.4
相似题
-
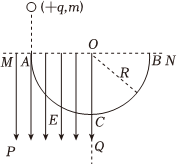 1.如图所示,ABC为光滑的固定在竖直面内的半圆形轨道,轨道半径为R=0.4m,A、B为半圆轨道水平直径的两个端点,O为圆心.在水平线MN以下和竖直线OQ以左的空间内存在竖直向下的匀强电场,电场强度E=1.0×106N/C.现有一个质量m=2.0×10-2kg,电荷量q=2.0×10-7C的带正电小球(可看作质点),从A点正上方由静止释放,经时间t=0.3s到达A点并沿切线进入半圆轨道,g=10m/s2,不计空气阻力及一切能量损失,求:
1.如图所示,ABC为光滑的固定在竖直面内的半圆形轨道,轨道半径为R=0.4m,A、B为半圆轨道水平直径的两个端点,O为圆心.在水平线MN以下和竖直线OQ以左的空间内存在竖直向下的匀强电场,电场强度E=1.0×106N/C.现有一个质量m=2.0×10-2kg,电荷量q=2.0×10-7C的带正电小球(可看作质点),从A点正上方由静止释放,经时间t=0.3s到达A点并沿切线进入半圆轨道,g=10m/s2,不计空气阻力及一切能量损失,求:
(1)小球经过C点时对轨道的压力大小;
(2)小球经过B点后能上升的最大高度.发布:2024/12/29 20:0:1组卷:750引用:4难度:0.5 -
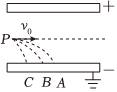 2.11H、12H、13H三个原子核,电荷均为e,质量之比为1:2:3,如图所示,它们以相同的初速度由P点平行极板射入匀强电场,在下极板的落点为A、B、C,已知上极板带正电,原子核不计重力,下列说法正确的是( )发布:2024/12/29 21:30:1组卷:374引用:5难度:0.6
2.11H、12H、13H三个原子核,电荷均为e,质量之比为1:2:3,如图所示,它们以相同的初速度由P点平行极板射入匀强电场,在下极板的落点为A、B、C,已知上极板带正电,原子核不计重力,下列说法正确的是( )发布:2024/12/29 21:30:1组卷:374引用:5难度:0.6 -
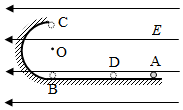 3.如图,在竖直平面内,一半径为R的半圆形轨道与水平轨道在B点平滑连接.半圆形轨道的最低点为B、最点高为C,圆心为O.整个装置处水平向左的匀强电场中.现让一质量为m、电荷量为q的带正电小球(可视为质点),从水平轨道的A点静止释放,到达B点时速度为.当小球过C点时撤去电场,小球落到水平轨道上的D点.已知A、B间的距离为5gRR,重力加速度为g,轨道绝缘且不计摩擦和空气阻力,求:103
3.如图,在竖直平面内,一半径为R的半圆形轨道与水平轨道在B点平滑连接.半圆形轨道的最低点为B、最点高为C,圆心为O.整个装置处水平向左的匀强电场中.现让一质量为m、电荷量为q的带正电小球(可视为质点),从水平轨道的A点静止释放,到达B点时速度为.当小球过C点时撤去电场,小球落到水平轨道上的D点.已知A、B间的距离为5gRR,重力加速度为g,轨道绝缘且不计摩擦和空气阻力,求:103
(1)该匀强电场场强E的大小;
(2)A、D间的距离;
(3)小球经过半圆形轨道某点P(图中未画出)时,所受合外力方向指向圆心O,求小球过P点时对轨道压力的大小.发布:2024/12/29 20:30:1组卷:59引用:2难度:0.7


