背景资料：在已知△ABC所在平面上求一点P，使它到三角形的三个顶点的距离之和最小．这个问题是法国数学家费马1640年前后向意大利物理学家托里拆利提出的，所求的点被人们称为“费马点”．如图1，当△ABC三个内角均小于120°时，费马点P在△ABC内部，当∠APB=∠APC=∠CPB=120°时，则PA+PB+PC取得最小值．
（1）如图2，等边△ABC内有一点P，若点P到顶点A、B、C的距离分别为3，4，5，求∠APB的度数，为了解决本题，我们可以将△APB绕顶点A旋转到△ACP'处，此时△ACP'≌△ABP这样就可以利用旋转变换，将三条线段PA、PB、PC转化到一个三角形中，从而求出∠APB=150°150°；
知识生成：怎样找三个内角均小于120°的三角形的费马点呢？为此我们只要以三角形一边在外侧作等边三角形并连接等边三角形的顶点与△ABC的另一顶点，则连线通过三角形内部的费马点．请同学们探索以下问题．
（2）如图3，△ABC三个内角均小于120°，在△ABC外侧作等边三角形△ABB'，连接CB'，求证：CB'过△ABC的费马点．
（3）如图4，在Rt△ABC中，∠C=90°，AC=1，∠ABC=30°，点P为△ABC的费马点，连接AP、BP、CP，求PA+PB+PC的值．
【考点】三角形综合题．
【答案】150°
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/25 8:0:9组卷：1616引用：4难度：0.1
相似题
-
1．（1）阅读理解：
如图1，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长AD到点E使DE=AD，连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是；
（2）问题解决：如图2，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF．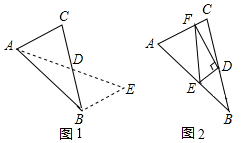
发布：2025/6/17 11:0:1组卷：624引用：7难度：0.4 -
2．如图，三角形ABO的三个顶点的坐标分别为O（0，0），A（5，0），B（2，4）．
（1）求三角形OAB的面积；
（2）若O，B两点的位置不变，点M在x轴上，则点M在什么位置时，三角形OBM的面积是三角形OAB的面积的2倍？
（3）若O，A两点的位置不变，点N由点B向上或向下平移得到，则点N在什么位置时，三角形OAN的面积是三角形OAB的面积的2倍？发布：2025/6/17 6:30:2组卷：331引用：2难度：0.3 -
3．如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE．
（1）求证：AD=BE；
（2）求∠AEB的度数；
（3）探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=90°，点A，D，E在同一直线上，CM⊥DE于点M，连接BE．
①∠AEB的度数为 °；
②线段DM，AE，BE之间的数量关系为 ．（直接写出答案，不需要说明理由）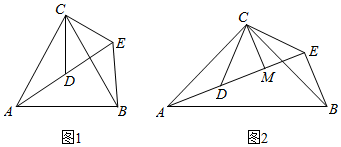
发布：2025/6/17 6:0:2组卷：365引用：3难度：0.6
