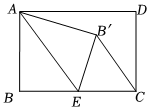
如图，在矩形ABCD中，AB=8，BC=12点E为BC的中点，将△ABE沿直线AE折叠，点B落在B'点处，连接B'C．
（1）线段BE=66，AE=88；
（2）判断AE与B'C的位置关系为 AE∥B'CAE∥B'C，并给出证明过程；
（3）若B'C=8，求△B'EC的面积．
【考点】翻折变换（折叠问题）；矩形的性质．
【答案】6；8；AE∥B'C
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/10 8:0:8组卷：60引用：1难度：0.7
相似题
-
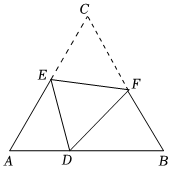1．点D是等边三角形ABC的边AB上的一点，且AD=1，BD=2，现将△ABC折叠，使点C与点D重合，折痕为EF，点E，F分别在AC和BC上，若BF=，则CE的长为（ ）54发布：2025/5/24 7:30:1组卷：157引用：3难度：0.6 -
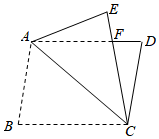2．如图，将平行四边形ABCD沿对角线AC翻折，使点B落在点E处，CE交AD于点F，若∠B=80°，∠ACE=2∠ECD，FC=a,FD=b,则平行四边形ABCD的周长为 ．发布：2025/5/24 8:0:1组卷：270引用：3难度：0.3 -
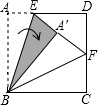3．如图，在正方形纸片ABCD上，E是AD上一点（不与点A，D重合）．将纸片沿BE折叠，使点A落在点A处，延长EA'交CD于点F，则∠EBF=（ ）发布：2025/5/24 8:0:1组卷：330引用：7难度：0.7
