问题情境：在学习了《勾股定理》和《实数》后，某班同学们以“已知三角形三边的长度，求三角形面积”为主题开展了数学活动，同学们想到借助曾经阅读的数学资料进行探究：
材料1．古希腊的几何学家海伦（Heron,约公元50年），在他的著作《度量》一书中，给出了求其面积的海伦公式S=p（p-a）（p-b）（p-c）（其中a,b,c为三角形的三边长，p=a+b+c2，S为三角形的面积）．
材料2．我国南宋时期数学家秦九韶曾提出利用三角形的三边长求面积的秦九韶公式：S=14[a2b2-（a2+b2-c22）2]，其中三角形边长分别为a,b,c,三角形的面积为S．
（1）利用材料1解决下面的问题：当a=5，b=3，c=25时，求这个三角形的面积？
（2）利用材料2解决下面的问题：已知△ABC三条边的长度分别是x+1，（5-x）2，4-（4-x）2，记△ABC的周长为C△ABC．
①当x=2时，请直接写出△ABC中最长边的长度；
②若x为整数，当C△ABC取得最大值时，请用秦九韶公式求出△ABC的面积．
S
=
p
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
p
=
a
+
b
+
c
2
1
4
[
a
2
b
2
-
（
a
2
+
b
2
-
c
2
2
）
2
]
a
=
5
c
=
2
5
x
+
1
（
5
-
x
）
2
4
-
（
4
-
x
）
2
【考点】三角形综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/24 6:0:4组卷：309引用：5难度：0.1
相似题
-
1．（1）阅读理解：
如图1，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．解决此问题可以用如下方法：延长AD到点E使DE=AD，连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是；
（2）问题解决：如图2，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF．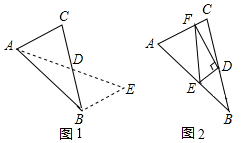
发布：2025/6/17 11:0:1组卷：624引用：7难度：0.4 -
2．如图，三角形ABO的三个顶点的坐标分别为O（0，0），A（5，0），B（2，4）．
（1）求三角形OAB的面积；
（2）若O，B两点的位置不变，点M在x轴上，则点M在什么位置时，三角形OBM的面积是三角形OAB的面积的2倍？
（3）若O，A两点的位置不变，点N由点B向上或向下平移得到，则点N在什么位置时，三角形OAN的面积是三角形OAB的面积的2倍？发布：2025/6/17 6:30:2组卷：331引用：2难度：0.3 -
3．已知，如图，在平面直角坐标系中，A为y轴正半轴上一点，B为x轴负半轴上一点．
（1）若BP平分∠ABO，AP平分∠BAO的外角，求∠P．
（2）如图2，C为x轴正半轴上一点，BP平分∠ABC，且P在AC的垂直平分线上．若∠ABC=2∠ACB，求证：AP∥BC．
（3）在第（2）问的条件下，D是AB上一点，E是x轴正半轴上一点，连AE交DP于H．当∠DHE与∠ABE满足什么条件时，DP=AE，请说明理由．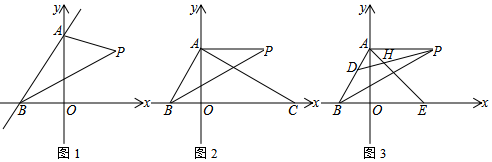
发布：2025/6/17 19:30:1组卷：75引用：1难度：0.3
