动量守恒定律的适用范围非常广泛,不仅适用于低速、宏观的问题,也适用于研究高速(接近光速)、微观(小到分子、原子的尺度)的问题。
(1)光滑水平面上,一个质量为m的小球以速度v碰撞竖直墙壁,碰后小球以相同的速度大小反弹。求此过程中小球的动量变化量Δp。
(2)气体对容器的压强是大量气体分子对容器壁的频繁撞击引起的。正方体密闭容器中有大量运动的粒子,每个粒子质量为m,单位体积内粒子数量为n。为简化问题,我们假定:粒子大小可以忽略;速率均为v,且与容器壁各面碰撞的机会均等;与容器壁碰撞前后瞬间,粒子速度方向都与容器壁垂直,且速率不变。推导容器壁受到的压强p与m、n和v的关系。
(3)可以认为光是由一个个不可分割的光子组成的。光子不仅具有能量,还具有动量。一个电子和一个正电子以相同的动能对心碰撞发生湮灭,转化为光子。这个过程能否只生成一个光子,并说明理由。
【答案】(1)此过程中小球的动量变化量Δp为-2mv。
(2)容器壁受到的压强p与m、n和v的关系为。
(3)过程不生成一个光子,理由是不符合动量守恒定律。
(2)容器壁受到的压强p与m、n和v的关系为
1
3
nm
v
2
(3)过程不生成一个光子,理由是不符合动量守恒定律。
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/4 8:0:5组卷:50引用:1难度:0.5
相似题
-
 1.如图所示,A球从距地面高h=2.5m处由静止释放,同时B球从地面上以v0=5m/s的速度竖直上抛,二者在同一直线上运动,经一段时间后二者发生弹性正碰,之后B与地面发生正碰时在某装置作用下迅速固定在地面上,已知两球完全相同,重力加速度g=10m/s2,不计空气阻力,在整个运动过程中,下列说法正确的是( )发布:2025/1/6 0:30:5组卷:107引用:3难度:0.5
1.如图所示,A球从距地面高h=2.5m处由静止释放,同时B球从地面上以v0=5m/s的速度竖直上抛,二者在同一直线上运动,经一段时间后二者发生弹性正碰,之后B与地面发生正碰时在某装置作用下迅速固定在地面上,已知两球完全相同,重力加速度g=10m/s2,不计空气阻力,在整个运动过程中,下列说法正确的是( )发布:2025/1/6 0:30:5组卷:107引用:3难度:0.5 -
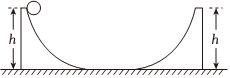 2.如图所示,光滑水平面上有两个相同的光滑弧形槽,左侧弧形槽静止但不固定,右侧弧形槽固定,两个弧形槽底部均与水平面平滑连接。一个小球从左侧槽距水平面高h处自由下滑,已知小球质量为m,弧形槽质量均为2m,下列说法正确的是( )发布:2024/12/28 1:0:7组卷:272引用:1难度:0.7
2.如图所示,光滑水平面上有两个相同的光滑弧形槽,左侧弧形槽静止但不固定,右侧弧形槽固定,两个弧形槽底部均与水平面平滑连接。一个小球从左侧槽距水平面高h处自由下滑,已知小球质量为m,弧形槽质量均为2m,下列说法正确的是( )发布:2024/12/28 1:0:7组卷:272引用:1难度:0.7 -
 3.“打羽毛球”是一种常见的体育健身活动。当羽毛球以4m/s的水平速度飞来时,运动员迅速挥拍以9m/s的水平速度迎面击球,假设羽毛球和羽毛球拍的碰撞为弹性碰撞,且球拍的质量远大于球的质量,请估算羽毛球反弹的速度大小为( )发布:2024/12/26 11:30:4组卷:104引用:2难度:0.8
3.“打羽毛球”是一种常见的体育健身活动。当羽毛球以4m/s的水平速度飞来时,运动员迅速挥拍以9m/s的水平速度迎面击球,假设羽毛球和羽毛球拍的碰撞为弹性碰撞,且球拍的质量远大于球的质量,请估算羽毛球反弹的速度大小为( )发布:2024/12/26 11:30:4组卷:104引用:2难度:0.8


