郑州东枫外国语学校八年级数学兴趣小组的同学们，对函数y=a|x-b|（a,b是常数，a≠0）的性质进行了初步探究，部分过程如下，请你将其补充完整．
（1）当a=1，b=0时，即y=|x|．当x≥0时，函数化简为y=x；当x＜0时，函数化简为y=-x-x．
（2）当a=2，b=1时，即y=2|x-1|．
①该函数自变量x和函数值y的若干组对应值如表：
| x | … | -2 | -1 | 0 | 1 | 2 | n | 4 | … |
| y | … | 6 | m | 2 | 0 | 2 | 4 | 6 | … |
其中m=
4
4
，n=3
3
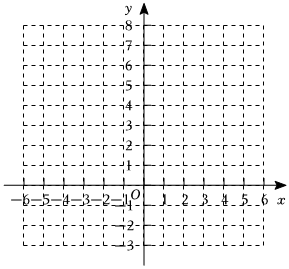
．②在图1所示的平面直角坐标系内画出函数y=2|x-1|的图象．
（3）请写出函数y=2|x-1|的一条性质：
当x=1时，y的值最小，最小值为0（答案不唯一，当x＜1时，y随x的增大而减小，当x＞1时，y随x的增大而增大等）．
当x=1时，y的值最小，最小值为0（答案不唯一，当x＜1时，y随x的增大而减小，当x＞1时，y随x的增大而增大等）．
．【答案】-x；4；3；当x=1时，y的值最小，最小值为0（答案不唯一，当x＜1时，y随x的增大而减小，当x＞1时，y随x的增大而增大等）．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/9 17:0:2组卷：212引用：2难度：0.8
相似题
-
1．如图，直线y=-x+2与x轴交于点A，与y轴交于点B，以点A为圆心，AB为半径画弧，交x轴于点C，则点C坐标为（ ）发布：2024/12/28 9:0:4组卷：320引用：3难度：0.6 -
2．如果点P（2，k）在直线y=-2x+2上，那么点P到x轴的距离为（ ）
发布：2024/12/23 12:0:2组卷：360引用：3难度：0.8 -
3．在直角坐标系中，等腰直角三角形A1B1O、A2B2B1、A3B3B2、…、AnBnBn-1按如图所示的方式放置，其中点A1、A2、A3、…、An均在一次函数y=kx+b的图象上，点B1、B2、B3、…、Bn均在x轴上．若点B1的坐标为（1，0），点B2的坐标为（3，0），则点An的坐标为（ ）发布：2024/12/23 12:30:2组卷：292引用：5难度：0.7
