如图1，在四边形ABCD中，AB=CD，E，F分别是BC，AD的中点，连接EF并延长，分别与BA，CD的延长线交于点M，N，则∠BME=∠CNE（不需证明）．
小明的思路是：在图1中，连接BD，取BD的中点H，连接HE，HF，根据三角形中位线定理和平行线性质，可证得∠BME=∠CNE．
问题：如图2，在△ABC中，AC＞AB，D点在AC上，AB=CD，E，F分别是BC，AD的中点，连接EF并延长，与BA的延长线交于点G，若∠EFC=60°，连接GD，判断△AGD的形状并证明．
【考点】三角形中位线定理；等边三角形的判定与性质．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：2289引用：4难度：0.1
相似题
-
1．如图，在四边形ABCD中，AB=AC，DB⊥AB，DC⊥AC，且E，F，G，H分别为AB，AC，CD，BD的中点．
（1）求证：EH=FG；
（2）连接AD，BC交于点O，则AD，BC有何关系，证明你的结论．发布：2025/6/23 15:0:2组卷：250引用：1难度：0.5 -
2．如图，D，E分别为△ABC的AC，BC边的中点，将此三角形沿DE折叠，使点C落在AB边上的点P处．若∠CDE=48°，则∠APD等于（ ）发布：2025/6/23 17:0:1组卷：1122引用：63难度：0.9 -
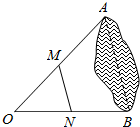3．如图，为估计池塘岸边A，B两点间的距离，在池塘的一侧选取点O，分别取OA，OB的中点M，N，测得MN=32m,则A，B两点间的距离是m.发布：2025/6/24 1:30:2组卷：1929引用：91难度：0.9
