【阅读理解】明朝数学家程大位在数学著作《直指算法统宗》中以《西江月》词牌叙述了一道“荡秋千”
问题：
| 原文：平地秋千未起，踏板一尺离地．送行二步与人齐，五尺人高曾记．仕女佳人争蹴，终朝笑语欢嬉．良工高士素好奇，算出索有几？ | 译文：将它往前推送10尺（水平距离）时，秋千的踏板就和人一样高，这个人的身高为5尺，秋千的绳索始终拉得很直，试问绳索有多长？（注古代5尺为1步） |
为了解决这个问题，需要依据问题建立数学模型．小明同学编写出了下列数学问题：
如图，秋千绳索OA静止的时候，踏板离地高一尺（AC=1尺），将它往前推进两步（EB=10尺），此时踏板升高离地五尺（BD=5尺）．已知：OC⊥CD于点C，BD⊥CD于点D，BE⊥OC于点E，OA=OB．求：秋千绳索（OA或OB）的长度．请你解答下列问题：
（1）四边形ECDB是
B
B
；A．一般平行四边形
B．矩形
C．菱形
D．正方形
（2）求OA的长．
【答案】B
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/12 8:0:9组卷：270引用：4难度：0.5
相似题
-
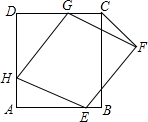1．如图，正方形ABCD边长为6．菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上，且AH=2，连接CF．
（1）当DG=2时，求证：菱形EFGH为正方形；
（2）设DG=x,试用含x的代数式表示△FCG的面积．发布：2025/6/16 0:30:2组卷：1629引用：5难度：0.7 -
2．如图1，在△ABC中，AB=AC，AD平分∠CAB，O是AB中点，连接DO，过点B作BE∥DA交DO的延长线于点E，连接AE．
（1）求证：四边形ADBE是矩形；
（2）当∠CAB=°时，四边形ADBE是正方形（直接填空）；
（3）如图2，若点F是BE边上一点（点F不与B、E重合）连接AF、DF，则图中与四边形ACDF面积相等的四边形 个．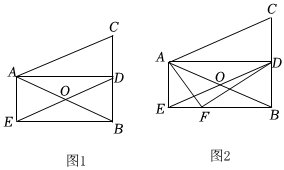
发布：2025/6/13 14:0:2组卷：65引用：1难度：0.5 -
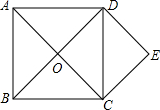3．如图，正方形ABCD的对角线AC与BD交于点O，过点C作CE∥BD，过点D作DE∥AC，CE与DE交于点E．
求证：四边形OCED是正方形．发布：2025/6/15 11:0:2组卷：1842引用：3难度：0.6
