当前位置：北师大新版八年级上册《5.1 认识二元一次方程组》2023年同步练习卷（3）> 试题详情

某单位组织34人分别到井冈山和瑞金进行革命传统教育，到井冈山的人数是到瑞金的人数的2倍多1人，求到两地的人数各是多少？设到井冈山的人数为x人，到瑞金的人数为y人，请列出满足题意的方程组
x
+
y
=
34
x
=
2
y
+
1
x
+
y
=
34
x
=
2
y
+
1
．

【考点】由实际问题抽象出二元一次方程组．

【答案】

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

当前模式为游客模式，立即登录查看试卷全部内容及下载

发布：2024/7/26 8:0:9组卷：630引用：55难度：0.7

相似题

1．某车间有60名工人生产太阳镜，1名工人每天可生产镜片200片或镜架50个．两个镜片和一个镜架配套，应如何分配工人生产镜片和镜架，才能使产品配套？设安排x名工人生产镜片，y名工人生产镜架，则可列方程组（　　）
A．
x
+
y
=
60
200
x
=
2
×
50
y
B．
x
+
y
=
60
2
×
200
x
=
50
y
C．
x
+
y
=
60
200
x
=
50
y
D．
x
+
y
=
60
200
x
=
1
2
×
50
y
发布：2025/6/8 3:30:1组卷：1613引用：14难度：0.7
解析
2．古代《永乐大典》中有一道趣题：钱二十贯，买四百六十尺，绫每尺四十三文，罗每尺四十四文，问绫、罗几何？意思是：用20贯钱买了460尺绫和罗，绫的价格是每尺43文，罗的价格是每尺44文，若设买了绫x尺，罗y尺，则用二元一次方程组表示题中的数量关系正确的是（说明：贯、文都是古代的一种货币单位，1贯=100文）（　　）
A．
x
+
y
=
460
43
y
+
44
x
=
20
B．
x
+
y
=
460
43
y
+
44
x
=
20000
C．
x
+
y
=
460
44
y
+
43
x
=
20
D．
x
+
y
=
460
44
y
+
43
x
=
20000
发布：2025/6/8 2:0:5组卷：38引用：1难度：0.7
解析
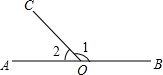3．如图所示，点O在直线AB上，OC为射线，∠1比∠2的3倍少10°，设∠1，∠2的度数分别为x,y,那么下列可以求出这两个角的度数的方程组是（　　）
A．
x
+
y
=
180
°
x
=
y
-
10
°
B．
x
+
y
=
180
°
x
=
3
y
-
10
°
C．
x
+
y
=
180
°
x
=
3
y
+
10
°
D．
3
y
=
180
°
x
=
3
y
-
10
°
发布：2025/6/8 4:0:1组卷：304引用：3难度：0.9
解析

某单位组织34人分别到井冈山和瑞金进行革命传统教育，到井冈山的人数是到瑞金的人数的2倍多1人，求到两地的人数各是多少？设到井冈山的人数为x人，到瑞金的人数为y人，请列出满足题意的方程组x+y=34x=2y+1x+y=34x=2y+1．

1．某车间有60名工人生产太阳镜，1名工人每天可生产镜片200片或镜架50个．两个镜片和一个镜架配套，应如何分配工人生产镜片和镜架，才能使产品配套？设安排x名工人生产镜片，y名工人生产镜架，则可列方程组（ ）

3．如图所示，点O在直线AB上，OC为射线，∠1比∠2的3倍少10°，设∠1，∠2的度数分别为x,y,那么下列可以求出这两个角的度数的方程组是（ ）

1．某车间有60名工人生产太阳镜，1名工人每天可生产镜片200片或镜架50个．两个镜片和一个镜架配套，应如何分配工人生产镜片和镜架，才能使产品配套？设安排x名工人生产镜片，y名工人生产镜架，则可列方程组（　　）

3．如图所示，点O在直线AB上，OC为射线，∠1比∠2的3倍少10°，设∠1，∠2的度数分别为x,y,那么下列可以求出这两个角的度数的方程组是（　　）