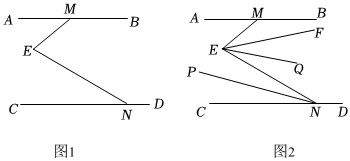
已知：直线AB∥CD，点M、N分别在直线AB，CD上，点E为平面内一点．
（1）如图1，猜想∠AME，∠MEN，∠ENC的数量关系并说明理由．
（2）利用（1）的结论解决问题：如图2，已知∠AME=40°，EF平分∠MEN，NP平分∠ENC，EQ∥NP，求∠FEQ的度数．
【考点】平行线的性质．
【答案】（1）∠MEN=∠AME+∠ENC，见解答过程；
（2）20°．
（2）20°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/4 8:0:9组卷：64引用：1难度：0.5
相似题
-
1．如图，AB∥CD，∠1=64°，FG平分∠EFD，则∠2=°．发布：2025/6/8 15:30:1组卷：44引用：3难度：0.9 -
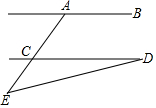2．如图所示，AB∥CD，∠CAB=116°，∠E=40°，则∠D的度数是（ ）发布：2025/6/8 15:30:1组卷：444引用：5难度：0.7 -
3．平面内的两条直线有相交和平行两种位置关系
（1）已知AB平行于CD，如a图，当点P在AB、CD外部时，∠BPD+∠D=∠B即∠BPD=∠B-∠D，为什么？请说明理由．如b图，将点P移动到AB、CD内部，以上结论是否仍然成立？若不成立，则∠BPD、∠B、∠D之间有何数量关系？请说明结论；
（2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系？（不需证明）
（3）根据（2）的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．
发布：2025/6/8 15:0:1组卷：759引用：2难度：0.3
