 阅读材料,并解决问题.
阅读材料,并解决问题.
【学习研究】我国古代数学家赵爽在其所著的《勾股圆方图注》中记载了一元二次方程的几何解法,以x2+2x-35=0为例,构造方法如下:
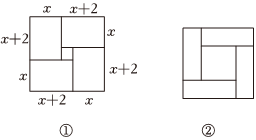
首先将方程x2+2x-35=0变形为x(x+2)=35,然后画四个长为x+2,宽为x的矩形,按如图①所示的方式拼成一个“空心”大正方形,则图①中大正方形的面积可表示为(x+x+2)2,还可表示为四个矩形与一个边长为2的小正方形面积之和,即4x(x+2)+22=4×35+4.因此,可得新方程(x+x+2)2=144.因为x表示边长,所以2x+2=12,即x=5.遗憾的是,这样的做法只能得到方程的其中一个正根.
【类比迁移】小颖根据以上解法解方程2x2+3x-2=0,请将其解答过程补充完整:
第一步:将原方程变形为x2+32x-1=0,即x( x+32x+32)=1;
第二步:利用四个全等的矩形构造“空心”大正方形;(在画图区画出示意图,标明各边长)
第三步:根据大正方形的面积可得新的方程 (x+x+32)2=4×1+(32)2(x+x+32)2=4×1+(32)2,解得原方程的一个根为 x=12x=12;
【拓展应用】一般地,对于形如x2+ax=b的一元二次方程可以构造图②来解.已知图②是由四个面积为3的相同矩形构成,中间围成的正方形面积为4,那么此方程的系数a=±2±2,b=33,求得方程的一个正根为 1或31或3.
x
2
+
3
2
x
-
1
=
0
3
2
3
2
3
2
3
2
3
2
3
2
1
2
1
2
【答案】x+;(x+x+)2=4×1+()2;x=;±2;3;1或3
3
2
3
2
3
2
1
2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/27 10:0:8组卷:270引用:3难度:0.5
相似题
-
1.某商场将每件进价为160元的某种商品原来按每件200元出售,一天可售出100件,后来经过市场调查,发现这种商品单价每降低1元,其销量可增加5件.
(1)求商场经营该商品原来一天可获利润多少元?
(2)若商场经营该商品一天要获利润4320元,则每件商品应降价多少元?发布:2025/6/10 3:30:1组卷:408引用:5难度:0.6 -
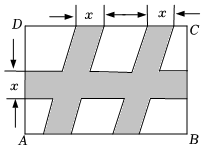 2.如图,世纪广场有一块长方形绿地,AB=18m,AD=15m,在绿地中开辟三条宽为xm的道路后,剩余绿地的面积为144m2,求道路宽x.发布:2025/6/9 23:30:1组卷:536引用:3难度:0.7
2.如图,世纪广场有一块长方形绿地,AB=18m,AD=15m,在绿地中开辟三条宽为xm的道路后,剩余绿地的面积为144m2,求道路宽x.发布:2025/6/9 23:30:1组卷:536引用:3难度:0.7 -
3.某商场以每件210元的价格购进一批商品,当每件商品售价为270元时,每天可售出30件,为了迎接“双十一购物节”,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价1元,那么商场每天就可以多售出3件.
(1)降价前商场每天销售该商品的利润是多少元?
(2)要使商场每天销售这种商品的利润达到降价前每天利润的两倍,且更有利于减少库存,则每件商品应降价多少元?发布:2025/6/10 4:30:1组卷:922引用:4难度:0.4


