请阅读下列材料：
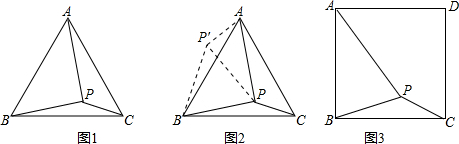
问题：如图1，在等边三角形ABC内有一点P，且PA=2，PB=3，PC=1、求∠BPC度数的大小和等边三角形ABC的边长．
李明同学的思路是：将△BPC绕点B逆时针旋转60°，画出旋转后的图形（如图2），连接PP′，可得△P′PB是等边三角形，而△PP′A又是直角三角形（由勾股定理的逆定理可证），所以∠AP′B=150°，而∠BPC=∠AP′B=150°，进而求出等边△ABC的边长为7，问题得到解决．
请你参考李明同学的思路，探究并解决下列问题：如图3，在正方形ABCD内有一点P，且PA=5，BP=2，PC=1．求∠BPC度数的大小和正方形ABCD的边长．
3
7
5
2
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/24 16:0:1组卷：1202引用：12难度：0.3
相似题
-
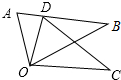1．如图，△ODC是由△OAB绕点O顺时针旋转30°后得到的图形，若点D恰好落在AB上，则∠A的度数为（ ）发布：2025/6/16 22:0:2组卷：1012引用：17难度：0.7 -
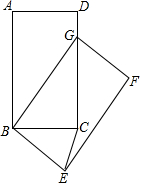2．如图，在矩形ABCD中，AB=5，BC=3，将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF，点G落在矩形ABCD的边CD上，连接CE，则CE的长是．发布：2025/6/17 1:30:2组卷：5886引用：20难度：0.5 -
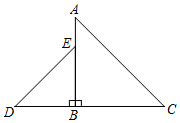3．如图，△ABC、△BDE都是等腰直角三角形，BA=BC，BD=BE，AC=4，DE=．将△BDE绕点B逆时针方向旋转后得△BD'E'，当点E'恰好落在线段AD'上时，则CE'=．22发布：2025/6/16 21:30:2组卷：451引用：3难度：0.4
