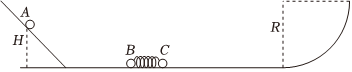
如图所示，一轻质弹簧的一端固定在球B上，另一端与球C接触但未拴接，球B和球C静止在光滑水平地面上。球A从光滑斜面上距水平地面高为H=5m处由静止滑下（不计小球A在斜面与水平面衔接处的能量损失），与球B发生正碰后粘在起，碰撞时间极短，稍后球C脱离弹簧，在水平地面上匀速运动后，进入固定放置在水平地面上的竖直四分之一光滑圆弧轨道内。已知球A和球B的质量均为1kg,球C的质量为3kg,且三个小球均可被视为质点，圆弧的半径

R

=

5

3

m

，g取10m/s²，求：
（1）球A到达斜面底部的速率；
（2）球C脱离弹簧后在圆弧上达到的最大高度h；
（3）调整球A释放初位置的高度H，球C与弹簧分离后恰好能运动至圆弧轨道的圆等高处。求球C在圆弧轨道内运动过程中克服重力做功的最大瞬时功率P。