已知,MN∥PQ,点A、点B分别在线段MN、PQ上.
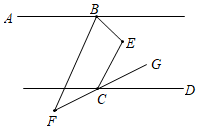
(1)如图1,点C在直线MN、PQ之间,求证∠ACB=∠NAC+∠QBC.
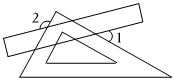
(2)如图2,分别过点A和点C作直线AG,CH,使AG∥CH,以点B为顶点作直角∠DBl,2并且∠DBl的两边分别与直线CH、AG交于点F和点E,则∠CFB+∠AEB=270°270°.(直接写出角度和)
(3)如图3,在(2)的条件下,若BD和AE恰好分别平分∠CBQ和∠CAM,并且∠ACB=106°,求∠CFB的度数.

【考点】平行线的性质.
【答案】270°
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/28 10:0:1组卷:246引用:1难度:0.5