图1是由若干个小圆圈堆成的一个形如等边三角形的图案，最上面一层有一个圆圈，以下各层均比上一层多一个圆圈，一共堆了n层．将图1倒置后与原图1拼成图2的形状，这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=n（n+1）2．
如果图3中的圆圈共有13层．
（1）我们自上往下，在每个圆圈中按图3的方式填上一串连续的正整数1，2，3，4，…，则最底层最左边这个圆圈中的数是 7979；
（2）我们自上往下，在每个圆圈中按图4的方式填上一串连续的整数-23，-22，-21，-20，…，求最底层最右边圆圈内的数是 6767；
（3）求图4中所有圆圈中各数值之和．（写出计算过程）
n
（
n
+
1
）
2
【考点】规律型：图形的变化类．
【答案】79；67
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/24 2:0:8组卷：730引用：8难度：0.3
相似题
-
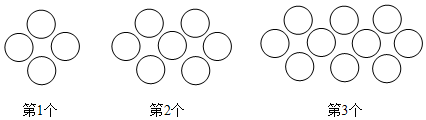
1．观察下列图形的构成规律，按此规律，第20个图形中棋子的个数为 ．
发布：2025/6/25 6:30:1组卷：53引用：2难度：0.5 -
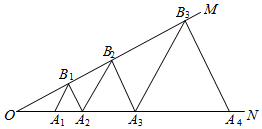2．如图，∠MON=30°，点A1，A2，A3，A4，…在射线ON上，点B1，B2，B3，…在射线OM上，且△A1B1A2，△A2B2A3，△A3B3A4，…均为等边三角形，以此类推，若OA1=1，则△A2021B2021A2022的边长为．发布：2025/6/25 8:30:1组卷：662引用：9难度：0.5 -
3．在同一平面内的n条直线两两相交，最多共有28个交点，则n=．
发布：2025/6/24 21:0:1组卷：215引用：5难度：0.7
