【知识生成】我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如图1可以得到（a+b）2=a2+2ab+b2，基于此，请解答下列问题：
【直接应用】（1）若x+y=5，xy=2，求x2+y2的值；
【类比应用】（2）若（x-3）（x-4）=1，求（x-3）2+（4-x）2的值；
以下是亮亮同学的解法：
解：∵（x-3）（x-4）=x2-7x+12=1，
∴x2-7x=-11，
∵（x-3）2+（4-x）2=x2-6x+9+16-8x+x2=2x2-14x+25，
∴（x-3）2+（4-x）2=2（x2-7x）+25=2×（-11）+25=3．
爱动脑筋的琪琪同学看了亮亮同学的解法后，灵机一动说到：“我还有其它不同的解法．”请你结合材料，类比第（1）题进行解答；
【知识迁移】（3）两块形状大小都相同的直角梯形（∠AOC=∠BCO=∠DOF=∠EFO=90°），如图2所示放置，其中A、O、F三点在同一直线上，连接AD、CF．若AF=14，每一个直角梯形的面积为69，且下底是上底的2倍，求△AOD与△COF的面积之和．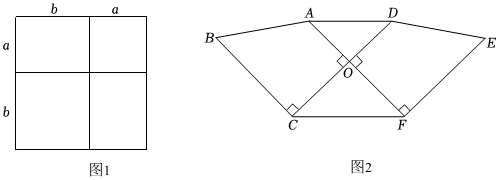
x
+
y
=
5
【答案】（1）1；
（2）3；
（3）52．
（2）3；
（3）52．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/10 3:0:1组卷：193引用：2难度：0.5
相似题
-
1．已知a=
，b=3+2，则2-3的值为（ ）1a+1b发布：2024/12/27 5:0:3组卷：1404引用：2难度：0.6 -
2．阅读理解：
若a=，b=15-3，求a2-ab+b2的值．15+3
解：∵a==15-3=5+3（5-3）（5+3），b=5+32=15+3=5-3（5+3）（5-3），5-32
∴a+b=，ab=5．12
∴a2-ab+b2=（a+b）2-3ab=5-=3272
请根据以上的解题提示，解答下列问题：
已知：x=，y=3-23+2，求3x2+5xy+3y2的值．3+23-2发布：2024/12/23 15:30:2组卷：105引用：1难度：0.9 -
3．已知
，x=3-7，求（x+y）2-3xy的值．y=7+3发布：2024/12/23 14:30:1组卷：265引用：7难度：0.7
