【问题背景】
△ABC中，BD是角平分线，点E是AB边上的一动点．
【初步探索】
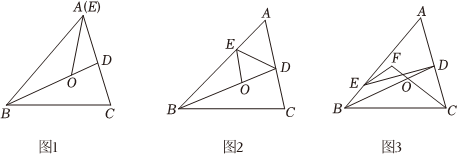
如图1，当点E与点A重合时，∠BED的平分线交BD于点O．
（1）若∠BAC=50°，∠ABC=60°，则∠EOD=5555°；
（2）若∠C=m°，则∠EOD=（90-12m）（90-12m）°；（用含m的代数式表示）
【变式拓展】
当点E与点A不重合时，连接ED，设∠ADE=α，∠ACB=β．
（1）如图2，∠BED的平分线交BD于点O．
①当α=50°，β=80°时，∠EOD=7575°；
②用α、β的代数式表示∠EOD=（90-12β+12α）°；（90-12β+12α）°；；
（2）如图3，∠ACB的平分线与BD相交于点O，与∠AED的平分线所在的直线相交于点F（点F与点E不重合），直接写出点F在不同位置时∠F与∠COD之间的数量关系．（用含α、β的代数式表示）
（
90
-
1
2
m
）
（
90
-
1
2
m
）
（
90
-
1
2
β
+
1
2
α
）
（
90
-
1
2
β
+
1
2
α
）
【答案】55；；75；°；
（
90
-
1
2
m
）
（
90
-
1
2
β
+
1
2
α
）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/30 8:0:9组卷：574引用：2难度：0.5
相似题
-
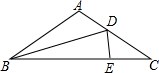1．已知：如图，△ABC中，∠ABC=∠C，BD是∠ABC的平分线，且∠BDE=∠BED，∠A=100°，求∠DEC的度数．发布：2025/1/24 8:0:2组卷：117引用：4难度：0.5 -
2．如图，在△ABC中，AE是中线，AD是角平分线，AF是高，则：
（1）∠BAC=2；
（2）BC=2；
（3）=90°．发布：2025/1/24 8:0:2组卷：45引用：1难度：0.5 -
3．如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…∠A2012BC和∠A2012CD的平分线交于点A2013，则：
（1）∠A1=度；
（2）∠A2013=度．发布：2025/1/24 8:0:2组卷：115引用：1难度：0.5
