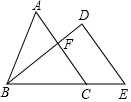
将一块直角三角板DEF放置在锐角△ABC上，使得该三角板的两条直角边DE、DF恰好分别经过点B、C．

（1）如图①，若∠A=40°时，点D在△ABC内，则∠ABC+∠ACB=
140
140
度，∠DBC+∠DCB=
90
90
度，∠ABD+∠ACD=
50
50
度；
（2）如图②，改变直角三角板DEF的位置，使点D在△ABC内，请探究∠ABD+∠ACD与∠A之间存在怎样的数量关系，并验证你的结论．

【答案】140；90；50

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/10/22 6:0:4组卷：204引用：2难度：0.5

相似题

1．已知在非直角三角形ABC中，∠A=45°，高BD与高CE所在直线交于点H，则∠BHC的度数是
．
发布：2025/6/16 17:30:2组卷：489引用：2难度：0.5
解析
2．如图，在△ABC与△DBE中，AC∥DE，点B，C，E在同一直线上，AC与BD相交于点F．若∠BDE=85°，∠BAC=55°，∠ABD：∠DBE=3：4，求∠DBE的度数
．
发布：2025/6/16 17:30:2组卷：38引用：1难度：0.7
解析
3．若一个三角形三个内角度数的比为2：3：4，则这个三角形是（　　）
A．直角三角形 B．等边三角形 C．钝角三角形 D．锐角三角形
发布：2025/6/16 16:30:1组卷：604引用：9难度：0.7
解析

1．已知在非直角三角形ABC中，∠A=45°，高BD与高CE所在直线交于点H，则∠BHC的度数是 ．