[实践操作]
在矩形ABCD中，AB=8，AD=6，现将纸片折叠，点D的对应点记为点P，折痕为EF（点E、F是折痕与矩形的边的交点），再将纸片还原．
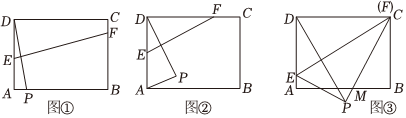
[初步思考]
（1）若点P落在矩形ABCD的边AB上（如图①）．当点P与点A重合时，∠DEF=9090°，当点E与点A重合时，∠DEF=4545°；
[深入探究]
（2）若点P落在矩形ABCD的内部（如图②），且点E、F分别在AD、DC边上，AP的最小值是 22；
[拓展延伸]
（3）若点F与点C重合，点E在AD上，射线BA与射线FP交于点M（如图③）．在各种不同的折叠位置中，是否存在某一情况，使得线段AM与线段DE的长度相等？若存在，请求出线段AE的长度；若不存在，请说明理由．
【考点】四边形综合题．
【答案】90；45；2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/11 8:0:9组卷：125引用：1难度：0.2
相似题
-
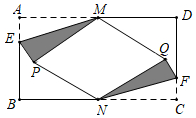1．综合与实践
问题情境：在数学活动课上，老师让同学们以“矩形的折叠”为主题开展数学活动如图，矩形纸片ABCD中，点M、N分别是AD、BC的中点，点E、F分别在AB、CD上，且AE=CF．
动手操作：将△AEM沿EM折叠，点A的对应点为点P，将△NCF沿NF折叠，点C的对应点为点Q，点P、Q均落在矩形ABCD的内部，连接PN、QM．
问题解决：（1）判断四边形PNQM的形状，并证明；
（2）当AD=2AB=4，四边形PNQM为菱形时，求AE的长．发布：2025/5/24 11:30:1组卷：112引用：2难度：0.3 -
2．【问题情境】
（1）如图1，在正方形ABCD中，E，F，G分别是BC，AB，CD上的点，FG⊥AE于点Q．求证：AE=FG．
【尝试应用】
（2）如图2，正方形网格中，点A，B，C，D为格点，AB交CD于点O．求tan∠AOC的值．
【拓展提升】
（3）如图3，点P是线段AB上的动点，分别以AP，BP为边在AB的同侧作正方形APCD与正方形PBEF，连接DE分别交BC、PC、AC于点M、N、H，求的值．S△ADHS△ABC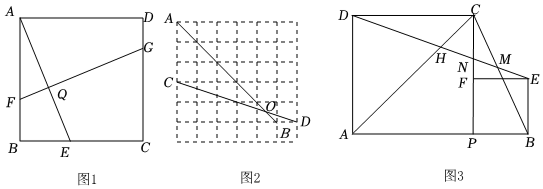
发布：2025/5/24 13:0:1组卷：430引用：1难度：0.3 -
3．在四边形ABCD中，AB=BC，∠B=60°；
（1）如图1，已知，∠D=30°求得∠A+∠C的大小为．
（2）已知AD=3，CD=4，在（1）的条件下，利用图1，连接BD，并求出BD的长度；
（3）问题解决；如图2，已知∠D=75°，BD=6，现需要截取某种四边形的材料板，这个材料板的形状恰巧符合如图2所示的四边形，为了尽可能节约，你能求出这种四边形面积的最小值吗？如果能，请求出此时四边形ABCD面积的最小值；如果不能，请说明理由．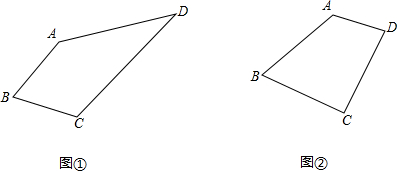
发布：2025/5/24 12:0:1组卷：527引用：3难度：0.1
