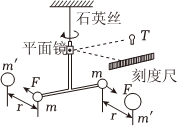
牛顿虽然发现了万有引力定律，却没能给出引力常量G的值。这是因为一般物体间的引力非常小，很难用实验的方法将它测量出来。1789年，英国物理学家 卡文迪什卡文迪什（选填“开普勒”或“卡文迪什”）巧妙地利用如图所示的扭秤装置，第一次在实验室比较准确地测出了引力常量G的值。已知T型架水平横梁长度为L，两端小球的质量均为m,位于同一水平面，当横梁处于平衡状态时，测得m,m'间的连线长度为r,引力大小为F，且与水平横梁垂直，则引力常量的表达式G=Fr2mm′Fr2mm′。
F
r
2
mm
′
F
r
2
mm
′
【考点】引力常量及其测定．
【答案】卡文迪什；
F
r
2
mm
′
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/16 8:0:9组卷：48引用：1难度：0.8
相似题
-
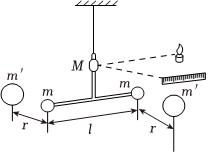1．牛顿虽然发现了万有引力定律，却没能给出引力常量G的值。这是因为一般物体间的引力非常小，很难用实验的方法将它测量出来。卡文迪什巧妙地利用如图所示的扭秤装置，第一次在实验室比较准确地测出了引力常量G的值，即G=6.67×10-11（选填“N⋅m2/kg2”或“N⋅m/kg”）。卡文迪什的实验涉及的物理思想方法是 （选填“等效替代法”或“微量放大法”）。发布：2024/12/29 22:0:2组卷：77引用：3难度：0.8 -
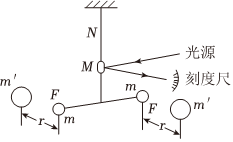2．如图所示，是卡文迪什测量万有引力常数的实验示意图，根据胡克定律及转动理论可知，两平衡球受到的等大反向且垂直水平平衡杆的水平力F与石英丝N发生扭转的角度Δθ成正比，即F=kΔθ，k的单位为N/rad,Δθ可以通过固定在T形架上平面镜M的反射点在弧形刻度尺上移动的弧长求出来，弧形刻度尺的圆心正是光线在平面镜上的入射点，半径为R。已知两平衡球质量均为m,两施力小球的质量均为m′，与对应平衡球的距离均为r,施加给平衡球的力水平垂直平衡杆，反射光线在弧形刻度尺上移动的弧长为Δl,则测得万有引力常数为（平面镜M扭转角度为Δθ时，反射光线扭转角度为2Δθ）（ ）发布：2024/7/12 8:0:9组卷：243引用：4难度：0.4 -
3．华中科技大学引力中心团队在引力常量的测量中作出了突出贡献，于2018年得到了当时最精确的引力常量G的值。下列说法正确的是（ ）
发布：2024/7/19 8:0:9组卷：96引用：2难度：0.9
