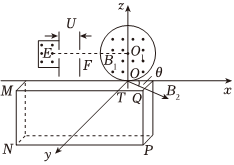
现代科学研究中经常利用电场、磁场来控制带电粒子的运动。在空间坐标系O-xyz中存在如图所示的电磁场，在xOz平面内，圆心O1的位置坐标为（0，R），半径为R，圆内存在垂直纸面向外的匀强磁场B1；在其左侧有一离子源E飘出质量为m、电荷量为q、初速度为0的一束正离子，这束离子经电势差U=mv202q的电场加速后，从小孔F（点F与O1等高）沿着x轴正方向射入匀强磁场区域B1，离子恰好从点O离开进入匀强磁场B2。竖直放置的长方形离子收集板MNPQ与xOz面相距R，边MQ足够长与x轴方向平行且与y轴交于点T，宽MN为2R，匀强磁场B2只局限于收集板正前方的空间区域，磁场方向与xOy所在平面平行且与x轴正方向的夹角大小为θ，调节匀强磁场的磁感应强度B2大小，使带正电离子偏转后能打到收集板上被吸收。不考虑离子重力和离子间的相互作用（已知：sin37°=0.6，cos37°=0.8，cos76°=0.25）
（1）求匀强磁场B1大小；
（2）若角度θ=0，求磁感应强度B2大小的范围；
（3）若角度θ=37°，磁感应强度B2=4mv05qR，求离子打在收集板上位置的坐标；
（4）若角度θ的大小在0到90°之间，试定量讨论磁感应强度B2的范围。
U
=
m
v
2
0
2
q
B
2
=
4
m
v
0
5
q
R
【答案】（1）匀强磁场B1大小为；
（2）若角度θ=0，求磁感应强度B2大小的范围为；
（3）若角度θ=37°，磁感应强度，离子打在收集板上位置的坐标为（，R，）；
（4）定量讨论磁感应强度B2的范围：①0≤θ≤60°时，
②60°≤θ≤76°时，
③76°≤θ≤90°时，无论B2取何值，粒子均无法打到收集板上。
m
v
0
q
R
（2）若角度θ=0，求磁感应强度B2大小的范围为
2
m
v
0
5
q
R
≤
B
2
≤
2
m
v
0
q
R
（3）若角度θ=37°，磁感应强度
B
2
=
4
m
v
0
5
q
R
-
3
R
4
-
5
R
4
（4）定量讨论磁感应强度B2的范围：①0≤θ≤60°时，
2
m
v
0
cosθ
q
R
（
4
co
s
2
θ
+
1
）
≤
B
2
≤
2
m
v
0
cosθ
q
R
②60°≤θ≤76°时，
m
v
0
2
q
R
≤
B
2
≤
2
m
v
0
cosθ
q
R
③76°≤θ≤90°时，无论B2取何值，粒子均无法打到收集板上。
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/5 8:0:9组卷：62引用：3难度：0.5
相似题
-
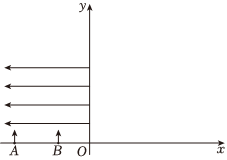1．在如图所示的平面直角坐标系中，第二象限内存在水平向左的匀强电场，在x轴上有两个粒子源A、B，沿y轴正向以相同速度同时发射质量相同、电荷量相同的带负电的粒子，粒子源A、B的坐标分别为xA=-9L、xB=-4L。通过电场后A、B两处发射的粒子分别从y轴上的C、D两点（图中未画出）进入第一象限。不计粒子重力及粒子间的相互作用。
（1）设C、D两点坐标分别为（0，yC）、（0，yD），求yC、yD的比值；
（2）若第一象限内未加任何场，两处粒子将在第一象限内某点相遇，求相遇点的横坐标；
（3）若第一象限内y＞yC区域，加上垂直于坐标平面方向向里的匀强磁场（图中未画出），两处粒子最终将从磁场飞出，求两处粒子飞出位置间的距离。发布：2024/12/29 20:30:1组卷：25引用：3难度：0.4 -
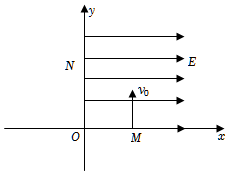2．如图，在xOy坐标系中的第一象限内存在沿x轴正方向的匀强电场，第二象限内存在方向垂直纸面向外磁感应强度B=的匀强磁场，磁场范围可调节（图中未画出）。一粒子源固定在x轴上M（L，0）点，沿y轴正方向释放出速度大小均为v0的电子，电子经电场后从y轴上的N点进入第二象限。已知电子的质量为m,电荷量的绝对值为e,ON的距离3mv02eL，不考虑电子的重力和电子间的相互作用，求：233L
（1）第一象限内所加电场的电场强度；
（2）若磁场充满第二象限，电子将从x轴上某点离开第二象限，求该点的坐标；
（3）若磁场是一个圆形有界磁场，要使电子经磁场偏转后通过x轴时，与y轴负方向的夹角为30°，求圆形磁场区域的最小面积。发布：2024/12/29 23:30:1组卷：256引用：5难度：0.3 -
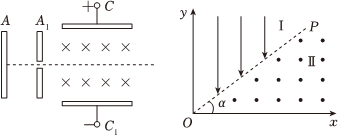3．在“质子疗法”中，质子先被加速到具有较高的能量，然后被引向轰击肿瘤，杀死细胞。如图所示，质量为m、电荷量为q的质子从极板A处由静止加速，通过极板A1中间的小孔后进入速度选择器，并沿直线运动。速度选择器中的匀强磁场垂直纸面向里，磁感应强度大小为B=0.01T，极板CC1间的电场强度大小为E=1×105N/C。坐标系xOy中yOP区域充满沿y轴负方向的匀强电场Ⅰ，xOP区域充满垂直纸面向外的匀强磁场Ⅱ，OP与x轴夹角a=30°。匀强磁场Ⅱ的磁感应强度大小B1，且1T≤B1≤1.5T。质子从（0，d）点进入电场Ⅰ，并垂直OP进入磁场Ⅱ。取质子比荷为，d=0.5m。求：qm=1×108C/kg
（l）极板AA1间的加速电压U；
（2）匀强电场Ⅰ的电场强度E1；
（3）质子能到达x轴上的区间的长度L（结果用根号表示）。发布：2024/12/29 20:30:1组卷：123引用：3难度：0.6
