1947 年德国学者阿尔弗德•莫斯纳发表了《一个神奇的幻方》，给出的一个如图 1 所示的 4 阶幻方（后被称为：莫斯纳幻方）。但国内有许多专业人都认为“莫斯纳幻方”源自如图 2 所示的“杨辉 4 阶幻方”。对“莫斯纳幻方”稍加分析后发现，它其实就是“杨辉 4 阶幻方”的一个变形：
（1）改变列的位置：将图 17-2 第 3 列变为图 17-1 第 1 列，第 1 列变为第 2 列，第 4 列变为第 3 列，第 2 列变为第 4 列。
（2）交换行的位置：经过（1）处理后幻方的第 1 行和第 4 行，第 2 行和第 3 行互换。

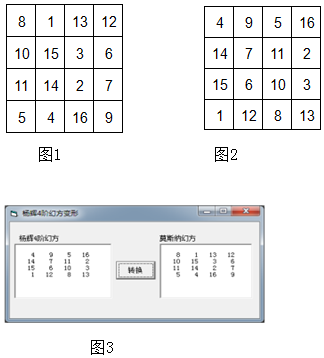
小李编写了一个将杨辉 4 阶幻方转换为莫斯纳幻方的 VB 程序，运行结果整齐地显示在列表框中，程序运行界面如图3 所示。请在横线处填入合适的代码。
Dim msy（1To 16）As Integer Dim msm（1To 16）As Integer
Function adj（c As Integer） As String'变量前添加适当的空格 Dim tmp1As String,n As Integer
tmp1=CStr（c）：n=5'CStr（x）函数是将数值变量 x 转换成字符串类型，并把前导空格删除。For i=1To n-Len（tmp1）
tmp1=““+tmp1Next i
adj=tmp1End Function
Private Sub Form_Load （　　）
'生成杨辉 4 阶幻方显示在 List1 中，并将数据按行依次放入 msy（1）至 msy（16）中，如 msy（1）=4，msy（2）=9
'上述操作代码略
End Sub
Private Sub Command1_Click （　　）
Dim pb As Integer,tmp As Integer,i As Integer,line As String For i=1To 16'变化列
If i Mod 4=1Then
 ①
ElseIf i Mod 4=3 Then
pb=i-2
Else
pb=pb+2
 End If
 ②
Next i
For i=1To 8'交换行
 If  ③Then
tmp=msm（i）：msm（i）=msm（i+12）：msm（i+12）=tmp
 Else
tmp=msm（i）：msm（i）=msm（i+4）：msm（i+4）=tmp
End If
Next i
line=““
List2．Clear
For i=1To 16
If i Mod 4=1
Then List2．AddItem line line=adj（msm（i））
Else
Line=line+adj（msm（i））
End If Next i
List2．AddItem line
End Sub