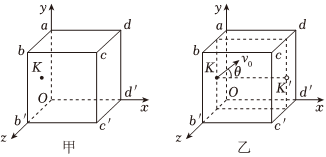
如图甲所示，空间直角坐标系Oxyz中，有一棱长为L的正方体区域，其中顶点a、b′、d′在坐标轴上。在平面Oabb′中心K点放置一装备，能沿各个方向发射电子。不考虑电子之间的相互作用。电子的质量为m,电子的电荷量为e。
（1）为了使初速度为v0，且平行x轴发射的电子不能到达平面dcc′d′，可在该空间范围内增加沿x轴方向的匀强电场，求该电场电场强度的最小值和方向；
（2）为了使初速度为v0，且平行x轴发射的电子不能到达平面dcc′d′，也可在该空间范围内增加垂直于x轴方向的匀强电场，求该电场电场强度的最小值；
（3）如图乙所示，K′位于K的正对面，虚线框平行于xy平面。电子以初速v0，且与KK′连线夹角为θ发射，在空间范围内增加垂直于x轴且和v0在同一个平面的匀强电场，该电子会从K′小孔离开，达到速度选择的功能。求该电子具有最大电势能时所在位置的电势。已知K所在位置为零势点。
【答案】（1）该电场电场强度的最小值为，方向为水平向右；
（2）该电场电场强度的最小值为；
（3）该电子具有最大电势能时所在位置的电势为。
E
=
m
v
2
0
2
e
L
（2）该电场电场强度的最小值为
2
m
v
2
0
e
L
（3）该电子具有最大电势能时所在位置的电势为
-
m
（
v
0
sinθ
）
2
2
e
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/5 8:0:2组卷：33引用：3难度：0.4
相似题
-
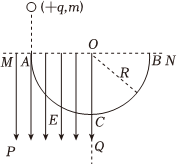1．如图所示，ABC为光滑的固定在竖直面内的半圆形轨道，轨道半径为R=0.4m,A、B为半圆轨道水平直径的两个端点，O为圆心．在水平线MN以下和竖直线OQ以左的空间内存在竖直向下的匀强电场，电场强度E=1.0×106N/C．现有一个质量m=2.0×10-2kg,电荷量q=2.0×10-7C的带正电小球（可看作质点），从A点正上方由静止释放，经时间t=0.3s到达A点并沿切线进入半圆轨道，g=10m/s2，不计空气阻力及一切能量损失，求：
（1）小球经过C点时对轨道的压力大小；
（2）小球经过B点后能上升的最大高度．发布：2024/12/29 20:0:1组卷：749引用：4难度：0.5 -
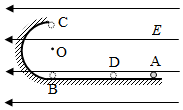2．如图，在竖直平面内，一半径为R的半圆形轨道与水平轨道在B点平滑连接．半圆形轨道的最低点为B、最点高为C，圆心为O．整个装置处水平向左的匀强电场中．现让一质量为m、电荷量为q的带正电小球（可视为质点），从水平轨道的A点静止释放，到达B点时速度为．当小球过C点时撤去电场，小球落到水平轨道上的D点．已知A、B间的距离为5gRR，重力加速度为g,轨道绝缘且不计摩擦和空气阻力，求：103
（1）该匀强电场场强E的大小；
（2）A、D间的距离；
（3）小球经过半圆形轨道某点P（图中未画出）时，所受合外力方向指向圆心O，求小球过P点时对轨道压力的大小．发布：2024/12/29 20:30:1组卷：58引用：2难度：0.7 -
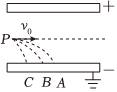3．11H、12H、13H三个原子核，电荷均为e,质量之比为1：2：3，如图所示，它们以相同的初速度由P点平行极板射入匀强电场，在下极板的落点为A、B、C，已知上极板带正电，原子核不计重力，下列说法正确的是（ ）发布：2024/12/29 21:30:1组卷：374引用：5难度：0.6
