对于平面直角坐标系xOy中的点M（a,b）和点N（a,b），给出如下定义：若满足b′=2m-b（b≥m） -b（b＜m）
，那么称点N是点M的“m-限变点”．
请解决下面的问题：
（1）当m=2时，
①已知点P的坐标是（2，1），则点P的“m-限变点”Q的坐标是 （2，-1）（2，-1）；
②若点P（a,b）的“m-限变点”Q的坐标为（-1，1），求点P的坐标；
（2）如图1，已知点A（1，5），B（4，2），点P在线段AB上，点P的“3-限变点”为Q，则Q的纵坐标t的取值范围是 -3＜t≤-2或1≤t≤3-3＜t≤-2或1≤t≤3；
（3）如图2，已知点P是一、三象限角平分线上的点，△ABC的顶点A（1，1）、B（4，-2）、C（6，0），若△ABC上存在点P的“m-限变点”，直接写出m的取值范围．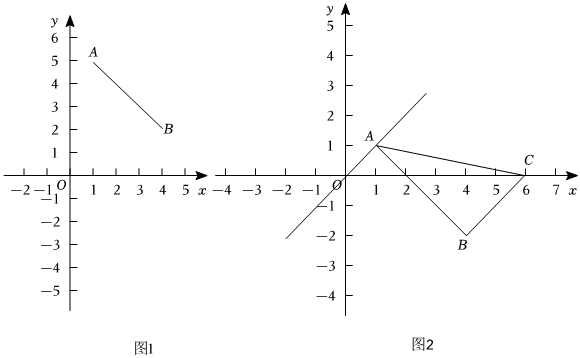
2 m - b （ b ≥ m ） |
- b （ b ＜ m ） |
【考点】三角形综合题．
【答案】（2，-1）；-3＜t≤-2或1≤t≤3
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/12 14:0:1组卷：82引用：1难度：0.3
相似题
-
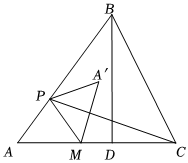1．在△ABC中，BD是AC边上的高，AD=3，CD=2，BD=4，点M在AD上，且AM=2．动点P从点A出发，沿折线AB-BD以每秒1个单位长度的速度运动，连结PM，作点A关于直线PM的对称点A′．设点P的运动时间为t秒（t＞0）．
（1）用含t的代数式表示线段BP的长；
（2）当点A′在△ABC内部时，求t的取值范围；
（3）连结CP．当CP⊥AB时，求△BCP的面积；
（4）当MA′∥AB时，直接写出t的值．发布：2025/6/9 21:30:1组卷：112引用：2难度：0.1 -
2．已知，点P为等边三角形ABC所在平面内一点，且∠BPC=120°．
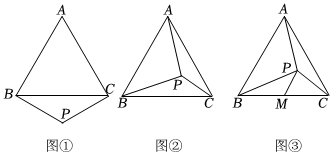
（1）如图（1），∠ABP=90°，求证：BP=CP；
（2）如图（2），点P在△ABC内部，且∠APB=90°，求证：BP=2CP；
（3）如图（3），点P在△ABC内部，M为BC上一点，连接PM，若∠BPM+∠APC=180°，求证：BM=CM．发布：2025/6/9 21:30:1组卷：242引用：2难度：0.1 -
3．如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=α．△COD为等边三角形，连接OD、AD．
（1）求证：△BCO≌△ACD；
（2）当α=150°时，试判断△AOD的形状，并说明理由；
（3）探究：当α为多少度时，△AOD是等腰三角形？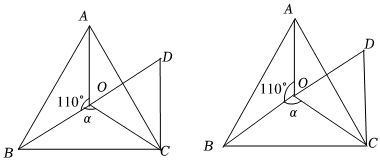
发布：2025/6/9 23:30:1组卷：57引用：2难度：0.4
