创意机器⼈⼤赛——捡硬币。⽐赛规则如下:
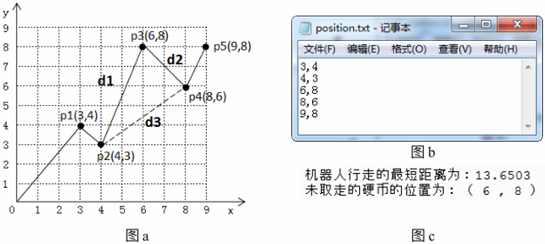
(1)在⽐赛场地上放置了n 个硬币,每个硬币的位置均不相同,各位置坐标(x,y)保存在⽂本⽂件中(如图所示,放置了5个硬币,⽂本中坐标按x,y 升序排列);
(2)机器⼈在两个硬币位置间⾛直线,从起点(0,0)出发,按硬币x 坐标从⼩到⼤去捡,若 x 坐标相同,则按 y 坐标从⼩到⼤捡;取⾛其中的n-1个硬币,总⾏⾛距离最短的机器⼈将获得⽐赛的冠军。
例:如图a 所示,p2直接到p4则代表p3处硬币未取。
完成该项⽬分以下⼏个步骤:
(1)读取坐标数据。
从⽂本⽂件中读取硬币的坐标(x、y),分别存储在列表x 和y 中。请在横线处填⼊合适的代码。

(2)编写函数,计算两点间的距离。请在横线处填⼊合适的代码。

(3)设计算法与程序实现。
机器⼈取⾛n-1个硬币经过的最短距离公式可以描述为:
其中:为机器⼈取⾛n-1个硬币⾛的最短距离;
为机器⼈取⾛n 个硬币经过的距离之和;
为机器⼈未取第i 个硬币少⾛的路程;
Max 为求中的最⼤值。
根据上述算法编写的Python 程序如下,请在横线处填⼊合适的代码。

(4)调试和异常处理。
当最后一个硬币未取为最短距离时,上述程序运⾏结果不正确。加框处代码有误,请修改。
【考点】事件处理过程.
【答案】(1)y.jye.ai(int(data[1]))
(2)sqrt((x2-x1)**2+(y2-y1)**2)或sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1))或((x2-x1)**2+(y2-y1)**2)**0.5
(3)①d1+d2-d3 ②long-maxd
(4)maxd=dist(x[n-2],y[n-2],x[n-1],y[n-1])
(2)sqrt((x2-x1)**2+(y2-y1)**2)或sqrt((x2-x1)*(x2-x1)+(y2-y1)*(y2-y1))或((x2-x1)**2+(y2-y1)**2)**0.5
(3)①d1+d2-d3 ②long-maxd
(4)maxd=dist(x[n-2],y[n-2],x[n-1],y[n-1])
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/6/27 10:35:59组卷:1引用:1难度:0.3
相似题
-
 1.汉诺塔问题如图所示,现要求将塔座A上的所有圆盘移到塔座B上,并仍按同样顺序叠放。移动圆盘时,需遵守汉诺塔问题的移动规则。由此,可设计出解汉诺塔问题的递归算法为( )发布:2024/11/14 8:0:1组卷:1引用:2难度:0.2
1.汉诺塔问题如图所示,现要求将塔座A上的所有圆盘移到塔座B上,并仍按同样顺序叠放。移动圆盘时,需遵守汉诺塔问题的移动规则。由此,可设计出解汉诺塔问题的递归算法为( )发布:2024/11/14 8:0:1组卷:1引用:2难度:0.2 -
2.有如下Python程序段:
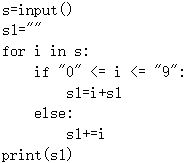
输入s值为“13Ka5iSh79“,执行该程序段后,输出的结果是( )发布:2025/1/2 9:0:7组卷:1引用:2难度:0.4 -
3.输出列表a中的元素的最大值。不要更改程序结构,将题中的①②③填入正确的语句。

(1)序号①答案为:。
A.range(1,5)
B.range(5)
C.a
D.a[4]
(2)序号②答案为:。
A.maxx+=1
B.k=maxx
C.maxx=k
D.k+=1
(3)序号③答案为:。
A.k
B.maxx
C.a[4]
D.a发布:2025/1/2 10:0:2组卷:3引用:2难度:0.4


