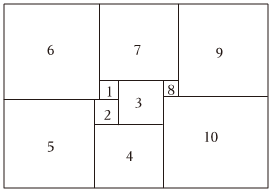
如图是1925年数学家莫伦发现的完美长方形，它恰能被分割成10个大小不同的正方形，其中正方形1，2的边长分别为x,y,则正方形3的边长为x+y,正方形4的边长为（x+y）+y=x+2y.
（1）用含x,y的代数式继续表示正方形5～9的边长；
（2）已知在完美长方形中，y=1.2x,则当x=5时，求这个完美长方形的周长．
【答案】（1）正方形5的边长为x+3y；正方形6的边长为4y；正方形7的边长为4y-x；正方形8的边长为3y-3x；正方形9的边长为7y-4x；正方形10的边长为10y-7x；（2）224．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/22 21:0:1组卷：25引用：2难度：0.5
