小刚同学听了“曹冲称象”的故事后，利用所学知识制作了一个“水秤”模型，可方便地称量物体的质量，其构造如图所示。已知透明大筒足够深，其底面积S=0.05m²，小筒的高度H=0.4m,底面积S₁=0.02m²，小筒和秤盘的总重为20N，小筒筒壁的厚度可忽略不计，假设在整个称量过程中小筒下表面始终与水面平行。
ρ_水=1×10³kg/m³。求：

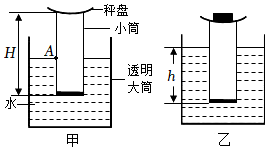
（1）该“水秤”的零刻度线应该在何处，即A点距小筒底部的距离。
（2）当该“水秤”达到最大称量限度时，小筒筒底受到水的压强。
（3）如图乙，在秤盘放上物体后，就可以称量物体所受的重力，某次该“水秤”称量一个体积为1.2×10^-2m³的实心木块时，该“水秤”模型恰好达到了最大称量限度，求木块的密度。