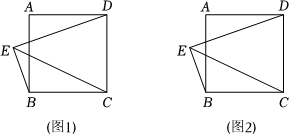
如图，点E为正方形ABCD外一点，连接BE，CE，DE．
（1）如图1，当∠CED=45°时，求证∠BEC=45°；
（2）如图2，当∠BEC=45°时，用等式表示线段BE，CE，DE之间的数量关系，并证明．

【答案】（1）见解析过程；
（2）DE+BE=

CE，理由见解析过程．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/6/27 10:35:59组卷：482引用：1难度：0.6

相似题

1．正方形ABCD中，两个顶点到直线l的距离相等，且均为另外两个顶点到直线l的距离的2倍，则这样的直线l有

条．
发布：2025/5/26 10:0:1组卷：87引用：2难度：0.7
解析
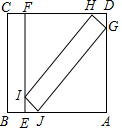2．有一个正方形ABCD，边长为1，其中有两个全等矩形BEFC，GHIJ，BE=
．
发布：2025/5/26 10:0:1组卷：434引用：1难度：0.4
解析
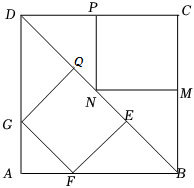3．如图，在正方形ABCD中，点F，M，P，G分别在边AB、BC、CD、DA上，点Q、N、E都在对角线BD上，且四边形GFEQ和CPNM均为正方形，则S_{正方形GFEQ}：S_{正方形CPNM}的值等于
．
发布：2025/5/26 9:30:1组卷：128引用：1难度：0.5
解析

如图，点E为正方形ABCD外一点，连接BE，CE，DE．（1）如图1，当∠CED=45°时，求证∠BEC=45°；（2）如图2，当∠BEC=45°时，用等式表示线段BE，CE，DE之间的数量关系，并证明．