当前位置：
试题详情
设a、b、c为平面上三条不同直线，
（1）若a∥b,b∥c,则a与c的位置关系是a∥ca∥c；
（2）若a⊥b,b⊥c,则a与c的位置关系是a∥ca∥c；
（3）若a∥b,b⊥c,则a与c的位置关系是c⊥ac⊥a．
【答案】a∥c；a∥c；c⊥a
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/27 14:0:0组卷：150引用：3难度：0.5
相似题
-
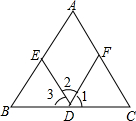1．如图，（1）因为∠A=（已知），
所以AC∥ED
（2）因为∠2=（已知），
所以AC∥ED
（3）因为∠A+=180°（已知），
所以AB∥FD
（4）因为AB∥（已知），
所以∠2+∠AED=180°
（5）因为AC∥（已知），
所以∠C=∠3．发布：2025/6/19 3:30:1组卷：571引用：4难度：0.5 -
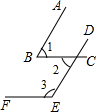2．如图，已知：AB∥DE，∠1+∠3=180°，
求证：BC∥EF．发布：2025/6/19 4:30:1组卷：383引用：9难度：0.5 -
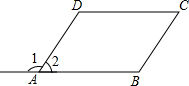3．如图，已知∠1=∠B，∠2=∠C，则下列结论不成立的是（ ）发布：2025/6/19 4:30:1组卷：546引用：22难度：0.9
