如图1,在Rt△ADC中,∠ADC=90°,延长CD至点B使DB=DA,线段DA上截取DO=DC,连接BO并延长交AC于点E.
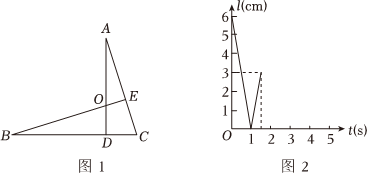
(1)判断线段BE与线段AC的位置关系 BE⊥ACBE⊥AC,并说明理由;
(2)有一动点Q从点A出发沿线段AC向点C匀速运动,QE的长度为l(cm)与点Q的运动时间为t(s)之间的图象如图2所示,请回答:
①点Q的运动速度为 66cm/s,BO的长度为 99cm;
②当△BOQ的面积为9cm2时,请求出t的值;
(3)若动点Q从点A出发沿射线AC匀速运动,另一动点P从点O出发沿线段OB向终点B匀速运动,P,Q两点同时出发,点P的运动速度小于点Q的速度,当点P到达点B时,P,Q两点同时停止运动.点F是直线BC上一点,且CF=AO.请直接写出:当△AOP与△FCQ全等时,线段AQ,AC,PO之间的数量关系.
【考点】三角形综合题.
【答案】BE⊥AC;6;9
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/15 8:0:9组卷:45引用:1难度:0.3
相似题
-
 1.综合与实践:
1.综合与实践:
问题情境:数学活动课上,王老师出示了一个问题:
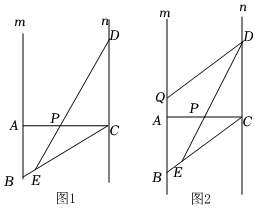
如图1,直线m∥n,点A、B在直线m上(点B在点A的下方),过点A作AC⊥n于点C,连接BC,以C为圆心CA为半径作弧,交直线n于点D,交BC于点E.求证:∠ABC=2∠CDE.
独立思考:(1)请解答王老师提出的问题.
实践探究:(2)DE与AC交于点P,在原有问题条件不变的情况下,王老师提出新问题,请你解答.
“猜想出AB、BC、PC的数量关系,并证明.”
问题解决:(3)过点D作DQ∥BC交m于点Q(点Q在点A上方),数学活动小组同学对上述问题进行特殊化研究之后发现,当AQ=BE时,线段BE和AB有一定的数量关系,该小组提出下面的问题,请你解答.
“如图2,当AQ=BE时,求的值.”DPAB发布:2025/6/14 20:0:1组卷:171引用:2难度:0.1 -
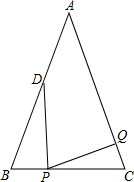 2.如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.
2.如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.
(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CPQ是否全等,请说明理由.
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为 cm/s时,在某一时刻也能够使△BPD与△CPQ全等.
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都按逆时针方向沿△ABC的三边运动.求经过多少秒后,点P与点Q第一次相遇,并写出第一次相遇点在△ABC的哪条边上?发布:2025/6/14 20:0:1组卷:112引用:2难度:0.3 -
3.如图1,在△ABC中,∠A=40°,外角平分线BN和CN相交于点N,求∠BNC的度数.
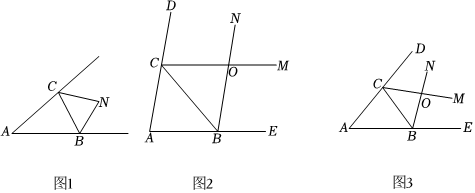
(1)请你先完成这个问题的解答.小明在完成以上问题的解答后,作如下变式探究:
(2)如图2,在△ABC中,∠A=80°,若∠CBN=∠CBE,∠BCM=38∠BCD,BN与CM交于点O,求∠BOC的度数.38
(3)如图3,在△ABC中,∠A=n°,若∠CBN=∠CBE,∠BCM=34∠BCD,当射线CM与BN相交时,n的取值范围是什么?试说明理由.34发布:2025/6/14 20:0:1组卷:257引用:2难度:0.4


