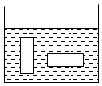
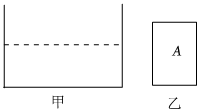
如图甲所示，放置在水平桌面上的薄壁圆柱形容器，高度为h₁，底面积为S₁，容器中装有某种未知液体，深度为4.8cm。另有一圆柱体A如图乙所示，底面积为S₂（S₁：S₂=5：2），圆柱体的高度为h₂（h₂＜h₁）。将柱体A轻放入容器中，A沉于容器底部且有一部分露出液面，将柱体A缓慢竖直向上提升，直到下表面高于容器底部3cm为止，A仍有部分浸入液体中，此时容器底部所受液体压强相对于放入柱体但未提升前减少了200Pa。（h₂＞2h₃）求：
（1）将柱体A轻放入容器后（A沉于容器底部且有一部分露出液面），容器中液体深度变为多少？
（2）液体的密度为多少？
（3）将容器中的原有液体倒出，倒入质量为m的另一未知液体，柱体A仍沉于容器底部且一部分露出液面，此时液体深度为h₃，容器底部所受液体压力为F₁，柱体对容器底部的压力为F₂，且F₂：F₁=2：5。向容器中继续加入该种液体，求容器中液体质量的最大值M（用m、h₁、h₂、h₃、S₁、S₂表示）。