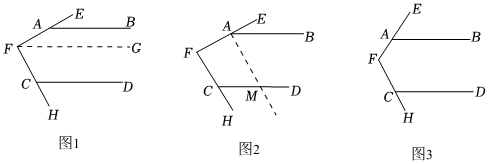
综合与实践：综合与实践活动课上，孙老师让同学们以“奇妙的平行线”为主题开展数学活动．如图1，∠EFH=90°，点A、C分别在射线FE和FH上，AB∥CD．
（1）若∠FAB=150°，则∠HCD=6060°；探究中小聪同学发现，过点F作FG∥AB即可得到∠HCD的度数，请直接写出∠HCD的度数；
（2）小明同学发现：无论∠FAB如何变化，∠FAB-∠HCD的值始终为定值，并给出了一种证明该发现的辅助线作法：如图2，过A作AM∥FH，交CD于M，请你根据小明同学提供的辅助线，先确定该定值，并说明理由；
（3）如图3，把“∠EFH=90°”改为“∠EFH=α”（0＜α＜180°），其它条件保持不变，猜想∠FAB与∠HCD的数量关系，并说明理由．
【考点】平行线的判定与性质．
【答案】60
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/26 8:0:9组卷：123引用：3难度：0.6
相似题
-
1．如图1，A、B分别是直线a和b上的点，∠1=∠2，C、D在两条直线之间，且∠C=∠D．
（1）证明：a∥b；
（2）如图2，∠EFG=60°，EF交a于H，FG交b于I，HK∥FG，若∠4=2∠3，判断∠5、∠6的数量关系，并说明理由；
（3）如图3，∠EFG是平角的n分之1（n为大于1的整数），FE交a于H，FG交b于I．点J在FG上，连接HJ．若∠8=n∠7，则∠9：∠10=．
发布：2025/6/17 14:30:2组卷：229引用：2难度：0.4 -
2．给出下列说法：
（1）两条直线被第三条直线所截，同位角相等；
（2）平面内的一条直线和两条平行线中的一条相交，则它与另一条也相交；
（3）相等的两个角是对顶角；
（4）三条直线两两相交，有三个交点；
（5）若a⊥b,b⊥c,则a⊥c.
其中正确的有个．发布：2025/6/17 14:30:2组卷：85引用：1难度：0.7 -
3．已知：如图，AE⊥BC，FG⊥BC，∠1=∠2，求证：AB∥CD．发布：2025/6/17 16:0:1组卷：2647引用：42难度：0.5
