甲、乙两辆汽车先后从A地出发到B地，甲车出发1h后，乙车才出发，如图所示的l1和l2表示甲、乙两车离出发地的距离y（km）与乙车行驶时间x（h）之间的关系．
（1）哪条线表示乙车离出发地的距离y与乙车行驶时间x之间的关系？
（2）甲、乙两车的速度分别是多少？
（3）试分别确定甲、乙两车离出发地的距离y（km）与乙车行驶时间x（h）之间的函数关系式．
（4）乙车能在1.5h内追上甲车吗？若能，说明理由；若不能，求乙车行驶几小时才能追上甲车．
【考点】一次函数的应用．
【答案】（1）l2表示乙车离出发地的距离y与追赶时间x之间的关系；
（2）甲车的速度为60km/h，乙车的速度为90km/h；
（3）乙车不能在1.5小时内追上甲车，乙车行驶2小时才能追上甲车．
（2）甲车的速度为60km/h，乙车的速度为90km/h；
（3）乙车不能在1.5小时内追上甲车，乙车行驶2小时才能追上甲车．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/27 8:0:9组卷：172引用：2难度：0.5
相似题
-
1．甲，乙两人从一条长为200m的笔直栈道两端同时出发，各自匀速走完该栈道全程后就地休息．图1是甲出发后行走的路程y（单位：m）与行走时间x（单位：min）的函数图象，图2是甲，乙两人之间的距离s（单位：m）与甲行走时间x（单位：min）的函数图象．
（1）求甲，乙两人的速度；
（2）求a,b的值．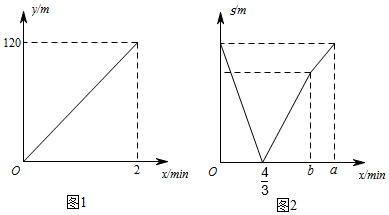
发布：2025/6/17 5:30:3组卷：715引用：8难度：0.7 -
2．如图是某出租车单程收费y（元）与行驶路程x（千米）之间的函数关系图象
，根据图象回答下列问题：
（1）当行驶8千米时，收费应为元；
（2）从图象上你能获得哪些信息（请写出2条）；
①；
②；
（3）求出收费y（元）与行驶x（千米）（x≥3）之间的函数关系式．发布：2025/6/17 6:0:2组卷：286引用：13难度：0.3 -
3．为了加强公民的节水意识，合理利用水资源，各地采用价格调控手段达到节约用水的目的，某市规定如下用水收费标准：每户每月的用水量不超过6立方米时，水费按每立方米a元收费，超过6立方米时，不超过的部分每立方米仍按a元收费，超过的部分每立方米按c元收费，该市某户今年5、6月份的用水量和所交水费如下表所示：
设某户每月用水量x（立方米），应交水费y（元）月份 用水量（m3） 收费（元） 5 5 7.5 6 9 27
（1）求a,c的值；
（2）当x≤6，x＞6时，分别写出y于x的函数关系式；
（3）该户11月份用水量为8立方米，求该户11月份水费是多少元？发布：2025/6/17 5:30:3组卷：194引用：8难度：0.3
