建筑是一门不断演化和创新的艺术，从古代的大理石殿堂到现代的钢铁森林，它的魅力在于其无限的可能性．近年来，一种名为双曲铝单板的新兴材料以其独特的曲线和光泽，为建筑注入了新的时尚元素，同时也赋予了建筑更多的创意和流动性．图2为某广东厂家设计制造的双曲铝单板建筑的横截面，可以看作由两条曲线EG、FH（反比例函数图象的一支）和若干线段围成，其中四边形ABDC与四边形GMNH均为矩形，AB=2m,BE=2m,AC=20m,GM=10m,MN=4m,如图2所示，取AC中点O，以点O为原点，AC所在直线为x轴建立平面直角坐标系．请回答下列问题：
（1）如图2，求EG所在双曲线的解析式．
（2）如图3，为在曲面实现自动化操作，工程师安装了支架EG，并加装了始终垂直于EG的伸缩机械臂PQ用来雕刻EG所在曲面的花纹，请问点P在EG上滑动过程中，PQ最长为多少米？
（3）如图4，为通风透气避免潮湿，在某一时刻，打开遮光板AC，太阳光线经点A恰好照射到点E，请求出此时线段HN上光线无法直射部分即线段KN的长．
【考点】反比例函数综合题．
【答案】（1）双曲线的表达式为；
（2）；
（3）8．
y
=
16
x
（2）
2
（3）8．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/4 14:0:2组卷：1230引用：4难度：0.2
相似题
-
1．模具厂计划生产面积为4，周长为m的矩形模具．对于m的取值范围，小亮已经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程如下：
（1）建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4，得xy=4，即y=；由周长为m,得2（x+y）=m,即y=-x+4x．满足要求的（x,y）应是两个函数图象在第 象限内交点的坐标．m2
（2）画出函数图象
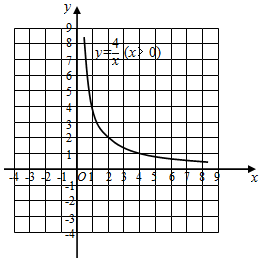
函数y=（x＞0）的图象如图所示，而函数y=-x+4x的图象可由直线y=-x平移得到．请在同一平面直角坐标系中直接画出直线y=-x.m2
（3）平移直线y=-x,观察函数图象
①当直线平移到与函数y=（x＞0）的图象有唯一交点（2，2）时，周长m的值为 ；4x
②在直线平移过程中，交点个数还有哪些情况？请写出交点个数及对应的周长m的取值范围．
（4）得出结论
若能生产出面积为4的矩形模具，则周长m的取值范围为 ．发布：2025/6/15 11:30:1组卷：4570引用：14难度：0.1 -
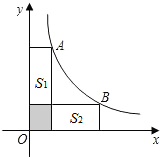2．如图，点A、B是双曲线y=上的点，分别经过A、B两点向x轴、y轴作垂线段，若S阴影=1，则S1+S2=．3x发布：2025/6/15 18:0:1组卷：1568引用：124难度：0.7 -
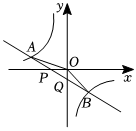3．如图，直线y=k1x+b与x轴、y轴相交于P，Q两点，与y=的图象相交于A（-2，m），B（1，n）两点，连接OA，OB．下列结论：①k1+k2＜0；②不等式k1x+b＞k2x的解集是x＞-2或0＜x＜1；③S△AOP=S△BOQ；④m+k2xn=0．其中正确的结论是（ ）12发布：2025/6/14 22:0:2组卷：2072引用：11难度：0.4
